Limita a srovnání

V této sekci se podíváme na vztah mezi srovnáním funkcí (pomocí nerovnosti) a srovnáním jejich limit.

Věta.
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f,g jsou funkce definované na nějakém prstencovém okolí a, předpokládejme, že f má v a limitu A a g má v a limitu B.
(i)     Jestliže existuje prstencové okolí a, na kterém f ≤ g, pak A ≤ B.
(ii)     Jestliže A < B, pak nutně existuje prstencové okolí a, na kterém f < g.

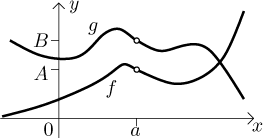
Tato tvrzení my měla vypadat rozumně, když si zkusíte nakreslit pár obrázků.

Může to být ještě jasnější, když si zkusíte představit opak. Zkuste nakreslit obrázek, kde f ≤ g, přesto je limita g ostře menší než limita f, brzy byste měli získat pocit, že to není možné.

Věta také platí pro nevlastní limity, předpokládá se přitom, že každé reálné číslo je větší než mínus nekonečno a menší než nekonečno. Jako obvykle je i tato věta pravdivá pro jednostranné limity po zjevných modifikacích (použijeme jednostranná prstencová okolí).

Mohlo by pomoci našemu chápání limity, jestliže se pokusíme nahlédnout, proč věta neříká víc. Začneme prvním tvrzením. Mohli bychom dostat lepší závěr, kdybychom v předpokladu použili ostrou nerovnost? Odpověď je záporná. I kdybychom věděli, že všude f < g, stejně bychom nemohli říct víc, než už je ve větě (třeba A < B vypadá lákavě, ale nejde to), protože i v takovém případě může pořád nastat A = B. Uvažujme například f (x) = x² a g(x) = 0 jako funkce na množině U = (−∞,0) ∪ (0,∞). Pak f < g na U, přesto mají obě limitu 0 v a = 0.

V druhém tvrzení je to podobné. Ostrá nerovnost je tam naprosto nutná, protože kdybychom ji zkusili trochu povolit, dostaneme se do problémů. Schválně si zkusme představit, že víme jen A ≤ B. Můžeme říct něco o f a g? Tentokráte uvažujme f (x) = x³ a g(x) = 0 jako funkce na množině U = (−∞,0) ∪ (0,∞). Jejich limity v bodě a = 0 jsou obě nulové, takže splňují podmínku A ≤ B, ale není možné udělat nějaké srovnání mezi f a g na žádném prstencovém okolí.

Větu jsme začali předpokladem, že máme limitu. Bez tohoto předpokladu není srovnání limit možné, protože jen ze srovnání mezi f a g nemůžeme odvodit existenci limity. Existuje ale výjimka.

Věta.
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f,g jsou funkce definované na nějakém prstencovém okolí bodu a, na kterém f ≤ g.
Jestliže f jde do nekonečna v a, pak také g jde do nekonečna v a.
Jestliže g jde do mínus nekonečna v a, pak také f jde do mínus nekonečna v a.

Mělo by to dávat smysl, v prvním případě f vytlačí g nahoru a přinutí ji jít do nekonečna, druhé tvrzení je opačná situace. Věta zase platí pro jednostranné limity.

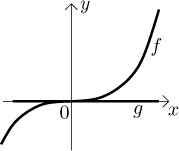
Jak je to s vlastními limitami? I kdybychom uzavřeli funkci shora a zdola konvergentními funkcemi, nemůžeme garantovat její konvergenci. Konec konců, víme, že omezené funkce nemusí konvergovat, například funkce sin(1/x) nemá limitu v 0, i když je omezená shora konstantní funkcí 1 (která v nule konverguje k 1) a zdola konstantní funkcí −1 (která v 0 konverguje k −1). Jestliže chceme vynutit konvergenci, nestačí omezit, musíme sevřít.

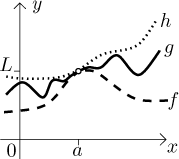
Tvrzení by zase mělo znít rozumně, když se podíváte na obrázek, g nemá jinou volbu než jít k L.

Tato věta má také verze s jednostrannými limitami. Funguje i pro nevlastní limity, ale pro ty je zbytečně komplikovaná, na ně máme lepší větu výše.

Věta o sevření má několik užitečných důsledků:

Věta (Věta o sevření - verze s absolutní hodnotou).
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f,g jsou funkce definované na nějakém prstencovém okolí a, na kterém | f | ≤ g. Jestliže g→0 v a, pak také f →0 v a.

Věta.
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f,g jsou funkce definované na nějakém prstencovém okolí a, předpokládejme, že je na něm f omezená.
(i)     Jestliže g→0 v a, pak f⋅g→0 v a.
(ii)     Jestliže |g|→∞ v a, pak f /g→0 v a.
(iii)     Jestliže g→∞ v a, pak f + g→∞ v a.

Tvrzení v (i) se často vyjadřuje slovy "nula krát omezená je nula", tvrzení v (ii) jako "nula dělená nekonečnem je nula"; dají se přidat mezi pravidla algebry limit.

Příklad: x⋅sin(1/x) konverguje k 0 v bodě a = 0, protože x jde k 0 v 0 a sin(1/x) je na svém definičním oboru omezený.

Pro tipy na správné použití sevření odkazujeme na Přehled metod, jmenovitě šuplík "srovnání a oscilace".

L'Hospitalovo pravidlo
Zpět na Teorie - Limita