Identity function and characteristic function

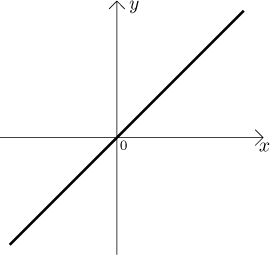
Definition.
The identity function, denoted Id, is defined for real numbers by

Id(x) = x.

The graph:

This is actually a familiar function, one of the simplest linear functions, so why do we single it out? It has a special meaning if we look at functions from the point of view of algebra and treat them as algebraic objects. Recall the concept of composition of functions. If we look at the properties of composition as an operation on a set of real functions, we find that it has some properties that we know from multiplication, but lacks others. We know that composition is not commutative, in fact compositions f ○ g and g ○ f are equal only in extremely rare cases, one has to do some work to come up with such an example. Similarly, there is no hope for the distributive law.

What does work? Composition is associative, that's one thing. Another interesting property is that, and here we are getting to it, it has a unity. By a unity we mean a certain element which, when applied (using the operation in question) to an arbitrary element, does not change it. With multiplication it is the number 1. Indeed, 1⋅x = x⋅1 = x for any real number x. For composition of functions, the role of unity is played exactly by the identity function Id. Indeed, for any function f and any x we have

f ○ Id: x ↦ f [Id(x)] = f [x],

which means that f ○ Id = f, and

Id ○ f: x ↦ Id[f (x)] = f (x),

which means that Id ○ f = f as well. By the way, the second equality above follows by realizing that the identity function Id is applied to a certain number f (x), and the action is that it leaves this number as it was.

We just showed that f ○ Id = Id ○ f = f for any real function f, so the identity function really serves as a unity for composition.

For the sake of completeness we remark that when we have a unity, we can ask for an inverse, and just like with multiplication of real numbers, we do have a notion of inverse element for functions and the composition. Indeed, the inverse function f₋₁ is an inverse to f in the algebraic sense, since the definition of the inverse function can be rewritten to mean f₋₁ ○ f = f ○ f₋₁ = Id. We know that not every function has an inverse, but that is nothing new, because also some real numbers do not have an inverse with respect to multiplication (namely, x = 0 is the culprit).

We actually cheated a bit here. The composition with inverse gives the identity function only if the function in question has the whole real line as both its domain and its range. On other cases we have to modify the equalities a bit, which brings us to the next topic.

Identity function on a set

Definition.
Let M be any subset of real numbers. We define its identity function Id_M by

Id_M(x) = x     for x from M.

So we have D(Id_M) = R(Id_M) = M.

Note that the identity function we introduced above is just a special case of this last definition, it is an identity function on the set of real numbers. Conversely, we can view Id_M as the restriction of Id to the set M. Now we can precisely write the definition of the inverse function: f₋₁ ○ f = Id_D( f ) and f ○ f₋₁ = Id_R( f )

Definition.
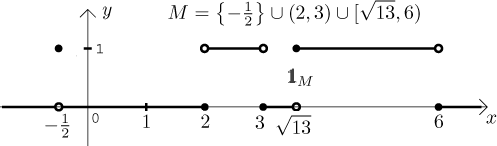
Let M be any subset of real numbers. We define its characteristic function by

The strange X is actually the Greek letter "chi". There is also an alternative notation, the characteristic function of a set M is denoted 1_M. It also has another name, some people call it the indicator function of the set M. A third possible notation is I_M, but it is perhaps the worst, since some people are lazy to write "d" and use just I_M for the identity function above, so it is easy to mix them up. The first notation is the most widespread, but since Greek letters are a real pain on the Web, I will use in Math Tutor the second one, with boldface 1.

Example: In the picture we show the graph of the characteristic function of the indicated set M.

Characteristic functions of sets are very useful, often they are used to express "restriction" of a function to some set. Why the quotes? Restriction means that we cut off some pieces of the domain. Here we have a situation when we keep the original domain, but we are only interested in the values of the function on some part of it, so we make the function zero elsewhere.

Precisely, let f be a function defined on some set M and let N be some subset of M. Let g be the function that has the same value as f on N but is zero elsewhere on M.

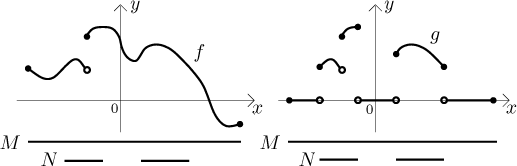
Then g can be written as g = f⋅1_N.

Indeed, if x is from N, then

[f⋅1_N](x) = f (x)⋅1_N(x) = f (x)⋅1 = f (x),

while for x that is from M but not from N we have

[f⋅1_N](x) = f (x)⋅1_N(x) = f (x)⋅0 = 0.

For another way of expressing characteristic function see the next section on the Heaviside function.

Heaviside function
Back to Theory - Elementary functions