Definition.
The Heaviside function is defined for real numbers by
![]()
Definition.
The Heaviside function is defined for real numbers by
Note that we did not make a typo, it really is Heaviside, not Heavyside.
In fact, it is a characteristic function of the interval
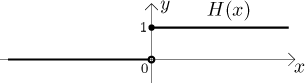
Some people also write
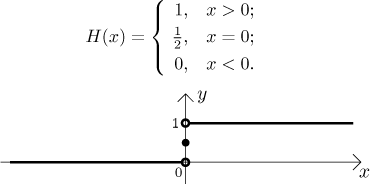
Since the Heaviside function is mostly used in situations when one point is irrelevant (namely in Laplace transforms), these two definitions lead to the same results.
Heaviside function is useful for writing characteristic functions of sets, most notably of intervals. Indeed, first note what a linear shift by c does:
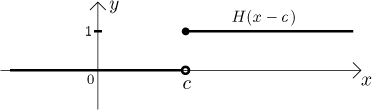
Now to get a characteristic function of an interval
![]()
This comes handy if we are only interested in values of a function f
on some interval
Again, in situations when the value at one point is not relevant we can use this trick to work with intervals of other kinds (open, closed).
Remark: What happens if we try to differentiate the Heaviside
function? For non-zero x the derivative is zero. The derivative at
In fact, the infinity is exactly of the right size that we get the Dirac delta function:
Definition.
The Dirac delta function is defined by the prescription
and the condition
The integral condition specifies how "large" the infinity should be. Of course, this is all nonsense, since a function cannot have infinity as its value and we do not know how to integrate such an object that we have here. However, there is a generalization of the notion of functions. Objects called distributions also include functions, but they allow more things to happen (like improper values), still most of the properties we have for functions work also for distributions. They are often used in specific applications, most notably in physics, and the Dirac delta function (properly Dirac distribution) is so useful for physicists and works so well that they call it a "function".
We include it here for the sake of completion, it is a rather weird object.
Apart from the fact that (in the world of distributions) we now have a cute
equality
![]()