Int(x) and Frac(x)

Definition.
Let x be a real number. We define its integer value as the largest integer Int(x) satisfying the condition Int(x) ≤ x.
We define its fractional value as Frac(x) = x − Int(x).

Examples: Int(3) = 3, Frac(3) = 0; Int(0.14) = 0, Frac(0.14) = 0.14; Int(17/8) = 2, Frac(17/8) = 1/8 = 0.125; Int(85263.781235) = 85263, Frac(85263.781235) = 0.781235.
Now it gets more interesting: Int(−1) = −1, Frac(−1) = 0; Int(−2.15) = −3 (really, −3 is the largest integer that is not larger than −2.15), Frac(−2.15) = 0.85; Int(−135.643) = −136, Frac(−135.643) = 0.357; Int(−117) = −117, Frac(−117) = 0.

You probably ask, why don't we define Int(x) as whatever is in front of the decimal point and Frac(x) as whatever is after the decimal point. Good question, I would like it that way, too. Unfortunately, such a definition would sometimes cause troubles, whereas the funny one that we put here is - from the mathematical point of view - without problems. One advantage we can show right away: The "right" definitions give much nicer graphs:

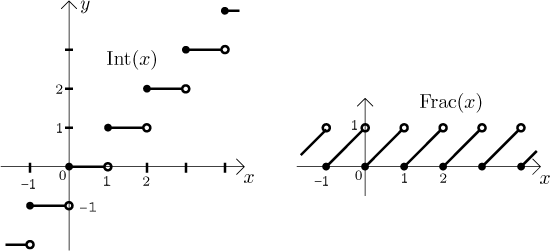
In fact, since we mostly use these functions for positive numbers, many people are not even aware that the definition behaves funny for negative numbers.

There is another justification for this definition. We can say that Int(x) is actually x rounded down to the nearest integer. There is also an alternative notation, Int(x) = ⌊x⌋. Similarly one can define ⌈x⌉ as x rounded up to the nearest integer.

Examples: ⌊13⌋ = 13, ⌈13⌉ = 13; ⌊13.7⌋ = 13, ⌈13.7⌉ = 14; ⌊−23⌋ = −23, ⌈−23⌉ = −23; ⌊−23.6⌋ = −24, ⌈−23.6⌉ = −23.

Factorial
Back to Theory - Elementary functions