Situace je následující: Chceme najít limitu v nějakém bodě a podílu
![]() či
či
![]() . Co se
dá dělat? Je několik alternativ.
. Co se
dá dělat? Je několik alternativ.
Toto je standardní postup.
Krok 1. Ověříme, že podíl f /g je v a typu
"nula nad nulou" nebo "nekonečno nad nekonečnem" (či obecněji
"něco nad nekonečnem").
Krok 2. Aplikujeme l'Hospitalovo pravidlo:
![]()
neboli zderivujeme čitatel a jmenovatel zlomku a pak zkusíme najít limitu
výsledného zlomku; pokud tato limita existuje, je to také odpověď na původní
problém.
Pokud limita napravo neexistuje, pak se o původním problému nedá nic říct.
Příklad:
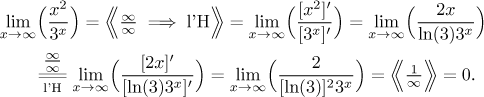
Všimněte si, že jsme museli použít l'Hospitalovo pravidlo dvakrát. To není
nic divného, pokud bychom tam měli
Poznámky:
1. Když aplikujeme l'Hospitalovo pravidlo, derivujeme zvlášť
čitatel a jmenovatel. Rozhodně nepoužíváme podílové pravidlo pro celý zlomek,
jak se o to někdy studenti pokoušejí. L'Hospitalovo pravidlo nemá nic
společného s derivováním daného výrazu, je to nástroj pro hledání limit,
který derivaci využívá svým způsobem. Samozřejmě pokud jsou výrazy v čitateli
a jmenovateli komplikovanější, pak při jejich derivování použijeme příslušná
pravidla.
2. Je naprosto zásadní ověřovat, zda opravdu máme neurčitý podíl (nebo obecněji zda g jde do nekonečna pro x jdoucí k a). Jinými slovy, v plné obecnosti toto pravidlo platí na dva typy: "nula dělená nulou" a "něco dělené nekonečnem". Pro ostatní typy toto pravidlo nefunguje, viz L'Hospitalovo pravidlo v části Teorie - Limita.
3. Ačkoliv l'Hospitalovo pravidlo funguje v mnoha případech a zdá se docela spolehlivé, není to univerzální řešení pro neurčitý podíl. Někdy jej nelze vůbec aplikovat, například pokud funkce f nebo g není diferencovatelná. Někdy lze l'Hospitalovo pravidlo použít, ale nepomůže, tj. nová limita, kterou dostaneme, není o nic lepší. Jeden z možných důvodů pro tuto situaci zde vysvětlíme: Síla l'Hospitalova pravidla spočívá v "zabíjecí" schopnosti derivace. Některé výrazy se ale derivováním nezlepší, pak l'Hospital často selže. Jsou dva populární případy:
Exponenciály se zachovávají. Příklad:
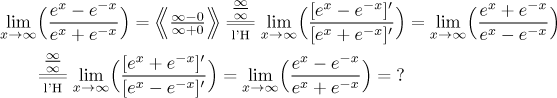
Na tuto limitu je lépe jít pomocí nástrojů ze šuplíku
"polynomy, sumy a podíly s mocninami v
nekonečnu", viz níže. Možná ale stojí za to udělat následující poznámku.
V této chvíli nevíme, zda limita existuje. Ale pokud ano, pak ji můžeme
nazvat L a ona rovnice, kterou jsme po prvním l'Hospitalovi dostali,
se dá přepsat jako
Odmocniny po derivaci nezmizí a obvykle se ještě zhorší. Další cyklický příklad:
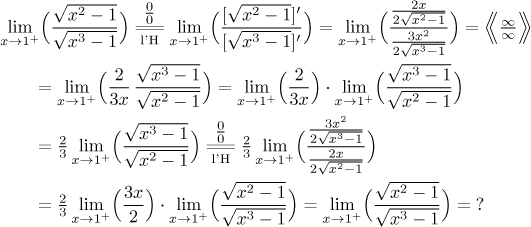
Zde je asi nejjednodušší zkrátit:
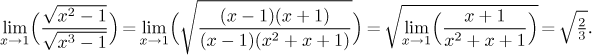
Pro mnohé neurčité podíly je tedy lepší poohlédnout se po alternativě.
Pokud limita také padne do šuplíku "polynomy, sumy a podíly s mocninami v nekonečnu", pak je většinou lepší použít nástroje z onoho šuplíku. Jako příklad se vrátíme k tomu s exponenciálami výše. Ve zlomku mají čitatel i jmenovatel stejný vedoucí člen, jmenovitě ex. Příslušná metoda volá po zkrácení tohoto členu:
![]()
I to je někdy možné. Jeden příklad jsme právě viděli, další je v šuplíku "polynomy ve vlastních bodech".
Jak už jsme zmínili, odmocniny jsou občas nepříjemné, když dojde na l'Hospitalovo pravidlo. Pokud jsou ty odmocniny nějak zamíchané v rozdílu, možná by se daly odstranit pomocí vhodného triku ze šuplíku "rozdíl odmocnin".
Téměř všechny příklady v části Řešené příklady zahrnují neurčitý podíl, tak se na ně podívejte.
Samozřejmě jsou také neurčité podíly, které nelze vyřešit oněmi čtyřmi přístupy a je třeba s nimi zatočit individuálně.
Další šuplík: neurčitý součin
Zpět na Přehled metod
- Limita