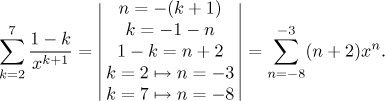Substituce

Substituce je obecná metoda používaná ke zjednodušení výrazů tím, že nějaké části přiřadíme jednoduché jméno.

Příklad: Uvažujme funkci

Pokud se rozhodneme označit y = x¹³, dostaneme

Jak vidíte, substituce se dělá prostým nahrazením. To je obecné pravidlo. Jsou dvě základní pravidla pro substituci.

1. Když se dělá substituce, původní proměnná musí zcela zmizet z daného výrazu.
2. Když nahrazujeme výskyty původní proměnné novou, můžeme použít pouze základní substituční rovnost a informace z ní odvozené.

Například v příkladu nahoře nás to může svádět k substituci y = 1 + x¹³. Teď víme, jak substituovat ve jmenovateli a v logaritmu, ale tato rovnice nám neumožní změnit ten sinus. Pravidlo 1 nám nicméně neumožňuje tam nechat x. Napovídá pravidlo 2, náhradu za x¹³ najdeme z původní substituční rovnosti.

y = 1 + x¹³, tedy x¹³ = y − 1.

Proto dostaneme

Jsou možné i komplikovanější výrazy, ale ať už při nahrazování použijeme jakékoliv vzorce, vždy musí být odvozeny z původní substituční rovnosti. Můžeme použít algebru, ale musíme být opatrní. Podívejme se na následující dva příklady.

Příklady:

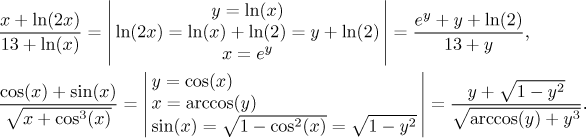
První substituce ukazuje, že je také možné při práci se substituční rovností přejít k inverzním funkcím. Druhá substituce ukazuje, že při tom musíme být opatrní.

Obecně, když děláme substituci, je její důležitou součástí to, pro jaké hodnoty proměnných se dělá. U toho příkladu na začátku jsme se o to moc nestarali, teď ale musíme. U té logaritmické substituce musíme zajistit, že ten logaritmus existuje, což znamená, že tu substituci můžeme udělat je pro x > 0. Musíme ale také být schopni přejít k inverzním funkcím, což je naštěstí pro nás možné na (0,∞). Toto naznačuje, že při substitucích dáváme přednost prostým funkcím.

To ale není vždy možné, jak vidíme u té kosinové substituce. Tam potřebujeme omezit x na nějakou množinu, na které je kosinus prostý. Typická substituce se dělá na nějakém intervalu, takže zde máme přirozeného kandidáta: x by mělo být z ⟨0,π⟩. Nabízí se ale i jiné intervaly a jejich volba může podstatně ovlivnit všechny následující výpočty. V našem případě je substituce tak, jak je napsaná, správně pouze pro tento interval. Pokud zvolíme jiný interval, kde je kosinus prostý, dopadne to jinak. Jestliže se například rozhodneme pracovat na [π,2π], musíme použít jinou inverzní funkci, jmenovitě x = 2π − arccos(y) (rozmyslete si to). Ve skutečnosti zde tedy máme nekonečně mnoho rozdílných substitucí, všechny jsou dané týmž vzorcem, ale liší se v intervalu, na kterých je děláme, a pro každý interval dostaneme pro x jiný výraz s arccos(y). Jak vidíte, ta substituce tak, jak byla napsaná, byla vlastně špatně, protože fungovala jen pro některá x, což tam mělo být specifikováno. Níže ukážeme, jak se to dá dělat.

Ale i kdybychom nemuseli přecházet k inverzní funkci, stejně je tam ještě jeden problém. Vzorec pro sinus s odmocninou funguje pouze za předpokladu, že sinus není záporný. Pokud omezíme x na ⟨0,π⟩, pak je toto splněno a substituce je správná tak, jak je napsaná. Když ale zkusíme ⟨π,2π⟩, pak je tam sinus nekladný a musíme to dělat jinak.

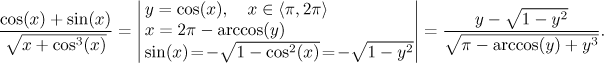
Ačkoliv většina substitucí takhle nezlobí, občas je nutné být opatrný, kde se pracuje.

Substituce a situace

Nikdy neděláme substituci jen tak, obvykle plánujeme s výrazem tropit nějakou matiku. To, jakou chceme dělat, pak definuje situaci pro výraz, a když děláme substituci, musíme odpovídajícím způsobem změnit i tu situaci. Pak občas mluvíme o "změně proměnné", protože spolu s výrazem také měníme celý problém do jazyka nové proměnné. Jsou tři populární situace.

Limity.
Když děláme substituci v limitě, musíme změnit všechny výskyty původní proměnné, což také zahrnuje to místo pod "lim". Tam prostě změníme jméno proměnné, ale vlastní limitní bod se musí změnit podle základní substituční rovnosti.

Příklad:

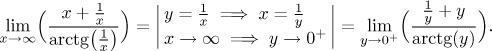
Derivace.
Když chceme derivovat funkci f (x) a použijeme substituci ke změně proměnné na y, musíme použít tento vzorec:

[ f (x)]′ = f ′(y)⋅y′.

Pak je nutno vrátit se k původní proměnné. Je to vlastně jen přeformulování řetízkového pravidla, tam najdete další informace.

Příklad: Uvažujme funkci

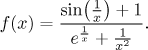
Jestliže chceme najít její derivaci, můžeme to udělat přímo, ale pak bychom museli použít řetízkové pravidlo na více místech. Možná bude snažší výraz nejprve zjednodušit substitucí:

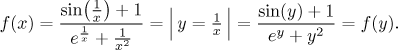
Teď snadno spočítáme

Nakonec použijeme pravidlo pro derivaci se substitucí:

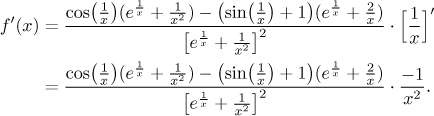
Integrace.
Jsou tři místa spojená se situací, kde se může objevit původní proměnná. Vždy je v "d"-členu (diferenciálu), například v dx, takže potřebujeme vědět, jak tohle změnit. Jestliže je integrál určitý, pak jsou i limity integrálu vzhledem k původní proměnné. Ty se změní na novou proměnnou snadno, prostě použijeme základní substituční rovnost.

Co se týče diferenciálu, je zde jednoduché pravidlo:

Substituce y = f (x) změní diferenciál takto: dy = f ′(x)dx.

Příklad:

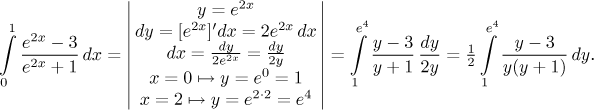
Protože integrace je silně specifická, odkazujeme na sekci substituce v části Integrály - Teorie - Metody pro další informace.

Sumy a řady.

Když měníme indexovací proměnnou v sumě (konečné či nekonečné), musíme také změnit její meze. Může také být nutné meze prohodit, protože na rozdíl od integrálu u sumy pořadí mezí nehraje roli a my vždy dáváme menší dolů.

Příklad: