Derivace a operace

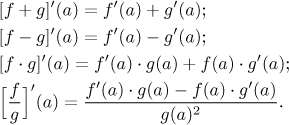
Algebraický přístup k derivaci potřebuje dvě komponenty. Tou první jsou elementární derivace, což jsou základní cihly, ze kterých se budou skládat derivace. Druhou ingrediencí je gramatika, pravidla, podle kterých budeme skládat elementární derivace. Jinými slovy, pořebujeme vědět, jak zderivovat funkci složenou z elementárních funkcí pomocí algebraických operací a kompozice. Nejprve se podíváme na lokální tvrzení.

Věta.
Předpokládejme, že funkce f a g jsou obě diferencovatelné v bodě a. Pak jsou funkce f  + g, f  − g a f ⋅g diferencovatelné v a a funkce f /g je diferencovatelná v a, pokud g(a) ≠ 0. Derivace navíc splňují

Příklad:

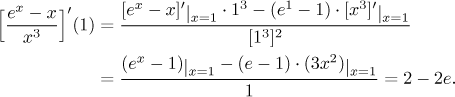
Věta.
Předpokládejme, že funkce f je diferencovatelná v a a že funkce g je diferencovatelná v b = f (a). Pak je složená funkce g ○ f = g( f ) diferencovatelná v a a

Všimněte si, že do g′ dosazujeme b, což je logické. Když si představíte, jak funkce jdou, uvidíte, že a žije v jiném prostoru, než kde má g svůj definiční obor, takže jej nemůžeme do g dosazovat.

Příklad:

Věta.
Předpokládejme, že funkce f a g jsou obě diferencovatelné na otevřené množině G. Pak jsou funkce f  + g, f  − g a f ⋅g diferencovatelné na G a funkce f /g je diferencovatelná na G za předpokladu, že g ≠ 0 na G. Derivace navíc splňují

Příklad:

Věta (řetízkové pravidlo).
Předpokládejme, že funkce f je diferencovatelná na otevřené množině G a že funkce g je diferencovatelná na množině f [G]. Pak je složená funkce g ○ f = g( f ) diferencovatelná na G a

Příklad:

Ještě se k tomuto příkladu vrátíme.

Používání těchto pravidel se dále věnujeme v části Přehled metod. Zde se na tato pravidla podíváme blíže. Začneme jednoduchým důsledkem.

Věta (derivace je lineární).
Předpokládejme, že funkce f a g jsou obě diferencovatelné na otevřené množině G a že A, B jsou reálná čísla. Pak

[Af  + Bg]′ = Af ′ + Bg′.

Tato věta je velmi důležitá, pokud chceme pracovat s derivací jako s transformací z jednoho prostoru funkcí (jmenovitě všechny funkce diferencovatelné na určité množině G tvoří lineární prostor) do jiného prostoru funkcí. Protože lineární transformace jsou "nejlepší", je pěkné vědět, že derivování tuto podmínku splňuje.

Zde se podíváme blíže na řetízkové pravilo. Zkusíme jej představit různými způsoby, protože to je pro studenty většinou na derivování to nejtěžší, na druhou stranu je to ve skutečnosti velice jednoduché, jde jen o pochopení. Jestli se vám zdá obtížné, když o něm slyšíte obvyklým způsobem, možná jej uvidíte lépe jiným způsobem.

Začneme poznámkou, že řetízkové pravidlo nám říká, co se stane s derivací funkce, když změníme proměnnou pomocí substituce. Pro jednoduchost teď budeme předpokládat, že všechny funkce, které zde zmíníme, jsou diferencovatlné všude, kde to potřebujeme.

Uvažujme funkci g, která závisí na proměnné y. Můžeme ji zderivovat, dostaneme tak g′(y). Co se stane, když pomocí substituce y = f (x) zavedeme novou proměnnou? Dostaneme novou funkci h(x) = g( f (x)). Jaká je její derivace? Samozřejmě, pokud máme tuto funkci dánu vzorcem, pak prostě spočítáme příslušnou derivaci, často ale potřebujeme obecný vzorec, který by ukázal, jak souvisí h ′ s g′. Řetízkové pravidlo říká, že

h ′(x) = g′(y)⋅f ′(x) = g′( f (x))⋅f ′(x).

To se dá přepsat takto:

Fakt.
Jestliže proměnná y závisí na jiné proměnné x, pak

[g(y)]′ = g′(y)⋅y′.

Abychom viděli, jak to funguje, vrátíme se k poslednímu příkladu, kde jsme chtěli derivaci sin(2x). Je to složená funkce. Když označíme y = 2x, dostaneme sin(y), což už není složená funkce, je to elementární funkce, jejíž derivaci si pamatujeme. Podle právě odvozeného pravidla tedy máme

[sin(2x)]′ = [sin(y)]′ = cos(y)⋅y′ = cos(2x)⋅[2x]′ = 2cos(2x).

Tohle se dá vlastně brát jako obecné pravidlo, opravdu existují učebnice, kde nemají elementární derivace jako ty v předchozí sekci, ale jejich seznam má řádky jako

[y^a]′ = ay^a−1⋅y′,       [e^y]′ = e^y⋅y′,       [sin(y)]′ = cos(y)⋅y′ atd.

Takové pravidlo také funguje pro "obyčejné" funkce, protože pokud je y základní proměnná, pak y′ = 1 a dostaneme [y ^a]′ = ay^a−1 atd. jako obvykle. Tyto vzorce jsou tedy zobecněním "našich" vzorců, fungují jak se základní, tak s transformovanou proměnnou.

Další zajímavý pohled na řetízkové pravidlo a substituci je pomocí Leibnizova značení. Pravidlo pak zní

Zdá se, jako by řetízkové pravidlo bylo jen krácení zlomků, protože levou stranu dostaneme vykrácením dy napravo. To je jen jedna z výhod, pokud předstíráme, že diferenciály existují (viz Leibnizovo značení). Když jsem se naučil kalkulus, bylo to neformálně na střední od učitele fyziky (potřebovali jsme to při řešení příkladů) a všechno vypadalo velice přirozeně. Krátíval jsem déčka napravo nalevo a nikdy to neselhalo. Pak jsem začal studovat matiku opravdu a dozvěděl jsem se, že to bylo špatně :-).

Ještě jedna poznámka. Proč se tomu říká řetízkové pravidlo? Odpoví následující část.

Jak fungují ona pravidla předvedená výše, když máme více funkcí? Linearita je pravidlo, které se hravě přizpůsobí více sčítancům i pro obecné transformace, takže to také musí platit pro derivování:

[A₁ f ₁ + A₂ f ₂ + ... + A_n f _n]′ = A₁ f ₁′ + A₂ f ₂′ + ... + A_n f _n′.

Máme také pravidlo pro součin více funkcí. Nejprve ukážeme formulku pro tři funkce, abychom ukázali hlavní myšlenku, a pak obecné pravidlo:

[ f ⋅g⋅h]′ =  f ′⋅g⋅h  +  f ⋅g′⋅h  +  f ⋅g⋅h′

[ f ₁⋅ f ₂⋅...⋅ f _n]′ =  f ₁′⋅ f ₂⋅...⋅ f _n +  f ₁⋅ f ₂′⋅...⋅ f _n + . . . +  f ₁⋅ f ₂⋅...⋅ f _n′

Poznamenejme, že není nutné si tato pravidla pamatovat, protože je hravě odvodíme z pravidel pro dvě funkce. Sčitání a násobení jsou totiž asociativní operace, takže můžeme doplnit závorky tak, abychom výraz změnili na sčítání/násobení dvou členů, a pak použijeme obvyklé pravidlo. Lepší než to komplikovaně vysvětlovat je ukázat příklad, odvodíme to pravidlo pro tři funkce.

[ f ⋅g⋅h]′ = [ f ⋅(g⋅h)]′ =  f ′⋅(g⋅h)  +  f ⋅[g⋅h]′
=  f ′⋅(g⋅h)  +  f ⋅(g′⋅h + g⋅h′) =  f ′⋅g⋅h  +  f ⋅g′⋅h  +  f ⋅g⋅h′.

Stejně tak není nutné si pamatovat pravidlo pro skládání více funkcí. Zase raději ukážeme verzi pro tři funkce, protože v obecném případě je značení dosti komplikované (příliš mnoho skládání a funkcí). Pokud pochopíte myšlenku, hravě najdete derivaci sta složených funkcí.

[h(g( f ))]′ = h′(g( f )) ⋅g′( f )⋅ f ′.

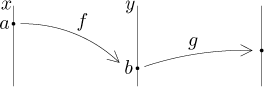
Jak vidíte, když máme řetěz složených funkcí jako na obrázku,

zderivujeme tu na konci (která se počítá naposled) a dosadíme do ní to, co tam bylo předtím. Pak si odmyslíme tu vnější funkci, kterou jsme právě zderivovali, a aplikujeme podobný proces na její vnitřek a znovu a znovu...

Příklad:

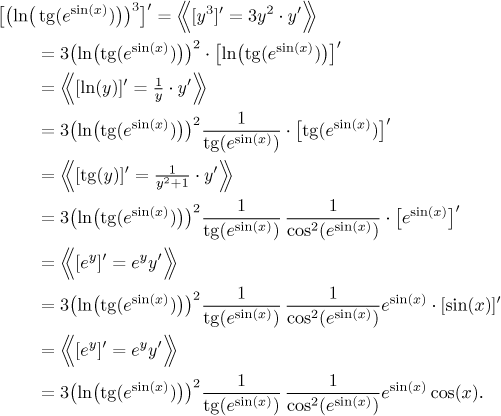
Teď vidíte, proč se tomu říká řetízkové pravidlo. Mimochodem, zkušený "derivovač" (či "derivátor" dle vzoru Terminátor) by vynechal všechny mezikroky a rovnou napsal odpověď, vytvářel by ji krok za krokem.

Mimochodem, protože dělení není asociativní operace, není ani pravidlo pro "více zlomků". Konec konců, co je to vlastně "více zlomků"? Protože na tohle není jasná odpověď, je jasné, že ani nemůže být pravidlo.

Linearita zase dělá iterování snadným. Pro k-tou derivaci máme

[Af  + Bg]^(k) = Af ^(k) + Bg^(k).

U součinu je to dost zajímavější, iterování součinového pravidla dává Leibnizův vzorec

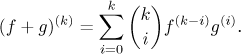
Například [ f  + g]′′ =  f ′′g + 2 f ′g′ + f g′′. Vypadá to povědomě? Taky by mělo! Zde je slavný binomicky vzorec pro k-tou mocninu:

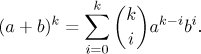
Úžasná shoda, že jo? Pro derivace vyššího řádu jiných operací vzorce nejsou.

Ačkoliv nalezení inverzní funkce (pokud vůbec existuje) není operace jako taková, derivování je moc pěkné a dovolí nám najít derivaci inverzní funkce pomocí derivace funkce původní.

Věta.
Předpokládejme, že f je funkce spojitá a striktně monotonní na nějakém okolí bodu a. Jestliže je f diferencovatelná v a a f ′(a) ≠ 0, pak je její inverze f ₋₁ diferencovatelná v b = f (a) a

Poznamenejme, že funkce ryze monotonní je už automaticky invertibilní. Abychom rozuměli tomu, proč dosazujeme právě to, co dosazujeme, podíváme se na obrázek naší situace:

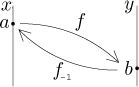
Je jasné, že b je to pravé místo, kde derivovat inverzní funkci, protože nemůže pracovat s a, které žije v jiném světe. Na druhou stranu, jediný rozumný kandidát na dosazení do f ′ je a. Jak by tento vzorec vypadal coby pravidlo?

Je to ještě zajímavější, když to přepíšeme pomocí Leibnizova značení. Máme y = f (x) a také x = f ⁻¹(y). Pravidlo pro inverzní funkci tedy zní

No není to pěkné? Abychom ukázali, jak se toto pravidlo používá, odvodíme vzorec pro derivaci logaritmu. Víme, že y = ln(x) je inverzní funkce k e ^y.

Zpět na Teorie - Derivace: Úvod