Problem: Evaluate (if it exists) the limit

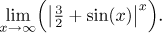
Solution: This is a standard problem, we want to find a limit at infinity of an expression that exists on a neighborhood of infinity (note that 3/2 + sin(x) > 0, so there will be no trouble when we change this general power into its canonical "e to ln" form). Thus we start by substituting infinity.

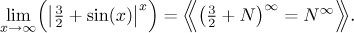
The expression N^∞ is indeterminate (see the algebra of N). When we change this general power into the canonical form, we get e^{xln(3/2 + sin(x))}, after substituting infinity we get ∞⋅ln(N) in the exponent, which is no help.

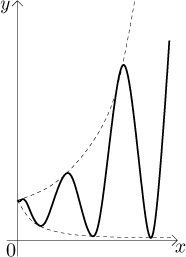
Thus standard methods fail and we need to look at the expression closer. What happens as x goes to infinity? The expression 3/2 + sin(x) keeps oscillating between 1/2 and 5/2 and we are raising these numbers to the power x. Thus the given expression sometimes looks like (1/2)^x, sometimes like (5/2)^x, and most of the time it looks like something between (in fact the graph of the given expression oscillates between the two exponentials).

Since |1/2| < 1, the exponential (1/2)^x tends to zero at infinity. On the other hand, since 5/2 > 1, the exponential (5/2)^x tends to infinity at infinity. The given expression oscillates between these two curves, therefore we would guess that it has no limit at infinity.

How would we prove it? The easiest way is to use the Heine theorem. We will consider two sequences that tend to infinity. With one sequence we will hit the tops, with the other the dips to show that the given expression has two different tendencies as x goes to infinity.

First, define x_n = π/2 + 2nπ. Then x_n→∞. When we substitute it into the given expression f (x), we get f (x_n) = (5/2)^{π/2 + 2nπ}→∞ as n goes to infinity.

On the other hand, we define y_n = 3π/2 + 2nπ. Then y_n→∞. When we substitute it into the given expression f (x), we get f ( y_n) = (1/2)^{3π/2 + 2nπ}→0 as n goes to infinity.

If f had a limit at infinity, then this limit would have to be equal to both infinity and 0, which is a contradiction.

For a different look at this example, see this problem in Sequences - Solved Problems - Limits.

Back to Solved Problems - Limits