Problem: Find the derivative of

Solution: We cannot take a derivative directly because of those absolute values, so we first have to get rid of them by considering all possibilities for sings of expressions inside these two absolute values. Breaking points are x = 0 and x = π. We get

(Perhaps a bit surprisingly we put equalities everywhere to remind the reader that there is no preference where we should put them, everybody can make his own choice. Indeed, for the breaking points both versions must yiled the same answer.) This is a function defined by cases. We can use rules to find derivatives at interiors of intervals in the description. First we will show in detail how we find the derivative for x < 0. There we differentiate the appropriate expression by rules.

By linearity, we differentiate each part separately. The first part is a cosine (whose derivative is minus sine) composed with an inside function, therefore we use the chain rule, differentiating the cosine first (it is done last). The second part is also a composition, so we use the chain rule with the outer function e^y whose derivative is e^y (again, it is done last when evaluating, so we start with it when differentiating). We get

The expression in the first derivative is again a composed function, the last operation (the outer function) is y⁵, so we apply the chain rule using [y⁵]′ = 5y⁴. The second differentiated expression is a linear expression whose derivative is elementary.

Finally we get the result, the derivative that remains takes on a linear expression.

Similarly we differentiate the expressions that define f on the remaining two open intervals, getting (try it)

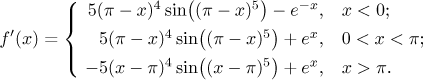
It remains to find out what is happening with the derivative at the breaking points. For that we use one-sided derivatives and the useful theorem (in Theory - MVT - Derivative and limit) that allows us to find these one-sided derivatives using limits of derivatives that we already calculated. One assumption of this theorem requires continuity of the given function at the investigated point, but this is true here, since originally we had one expression with absolute values which is continuous everywhere.

First we check on the origin.

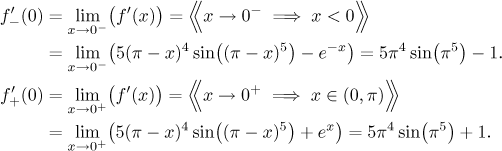
Since the two one-sided derivatives are not equal, there is no derivative at x = 0.

Now we check on pi.

Since the two one-sided derivatives are equal, we get derivative at π. We note that both expressions for the derivative used in limits can be also used at π, so we do not have to list the derivative at π as a separate case, but include it into one or even both relevant intervals (it comes to the same). We get

Next problem
Back to Solved Problems - Derivative