Derivative is one of the crucial tools for evaluating limits, namely l'Hospital's rule. Conversely, the most usual way of finding one-sided derivatives is via limits. We start with the latter.
Theorem.
Let f be a function continuous at a point a from the right and differentiable on some right reduced neighborhood of a. Then
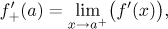
assuming that the limit exists.
Let f be a function continuous at a point a from the left and differentiable on some left reduced neighborhood of a. Then
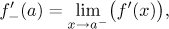
assuming that the limit exists.
Example:
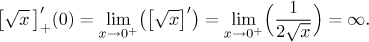
The main advantage of this approach is that we can use the algorithmic way of differentiation (rules), which is usually way simpler then going by definition. In this particular example the definition is not too bad either, see the section Derivative in Theory - Introduction.
Note that the above theorem looks really nice when we use the short notation for one-sided limit:
f ′+(a) = f ′(a+) and f ′-(a) = f ′(a-).
Theorem (l'Hospital's rule).
Let a be a real number, ∞, or −∞. Let f,g be functions defined on some reduced neighborhood of a. Assume that one of the following two conditions is satisfied:
(1) Both f and g converge to 0 at a;
(2) |g| tends to ∞ at a.
Then
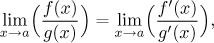
if the limit on the right exists.
Analogous theorem also works for one-sided limits. The proof of this theorem is based on the Cauchy theorem from the previous section. Since this theorem is so important for limits, we prefer to comment on it in the section l'Hospital rule in Functions - Theory - Limits.
Derivative and monotonicity
Back to Theory - Mean value theorem
