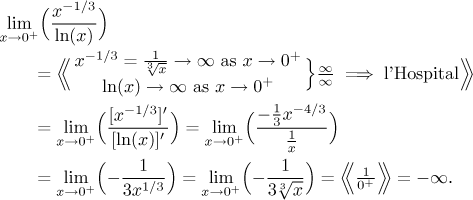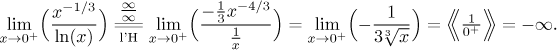First we recall the l'Hospital theorem from the section Derivative and limit in Derivative - Theory - MVT.
Theorem (L'Hospital's rule).
Let a be a real number, ∞, or −∞. Let f,g be functions defined on some reduced neighborhood of a. Assume that one of the following two conditions is satisfied:
(1) Both f and g converge to 0 at a;
(2)|g| tends to ∞ at a.
Then
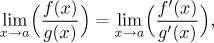
if the limit on the right exists.
Analogous theorem also works for one-sided limits. Note that the equality is "conditional", these two limits are equal only if the right one exists, otherwise the equality need not be true.
This rule is very important. When evaluating limits of fractions, we
often get an
indeterminate ratio, that is,
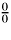or
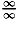. What a
coincidence, l'Hospital's rule helps us in these two cases. If we try to
evaluate a limit of a fraction and end up with zero over zero, then the
assumption (1) is satisfied and instead of evaluating the given limit we
evaluate the limit of the ratio of derivatives. If we have two infinities,
then the assumption (2) in the theorem is true and again we pass to
derivatives.
In fact, these two cases are so important that many authors simply state the l'Hospital rule precisely for these two cases, zero over zero and infinity over infinity. Most of the time the "simple" version works well enough, so those authors do not cheat their readers too much, but there are limits when one is grateful for the more general version, for instance if we face a fraction where the denominator gives infinity but the numerator has no limit at all. However, this does not happen often.
Example:
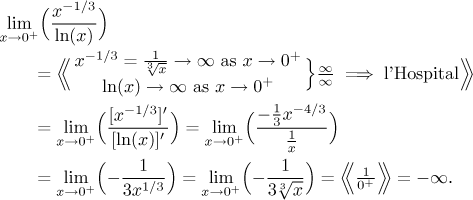
Since we got a definite answer at the end, the "conditional equality" in the l'Hospital rule step is justified. In practice we do not write all the details, in fact there is no generally accepted way of indicating the use of l'Hospital's rule. Here we will write it like this:
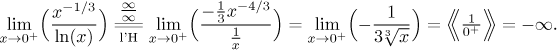
Now consider this
Example:
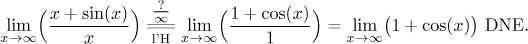
Since the limit at the end does not exist, the "conditional equality" need not be true and the given limit can be anything. In fact, using the "bounded divided by infinity gives zero" rule we get that
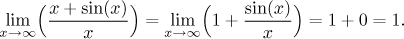
Of course, if the assumptions of the theorem are not satisfied, then the l'Hospital rule does not work. For instance, the following limit is obviously 1, but if we mistakenly use l'Hospital's rule (we forget to check whether the type of the limit is "zero over zero" or "something over infinity"), we get a wrong answer.
For practical tips on l'Hospital's rule see indeterminate ratio in Methods Survey.
