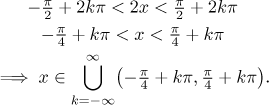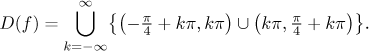Příklad: Najděte definiční obor a limity v krajních bodech jeho intervalů funkce

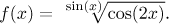
Řešení: Tato funkce je obecná mocnina, takže abychom ji mohli zkoumat, musíme ji nejprve převést na její kanonický tvar.

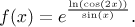
Teď se podíváme, jaké podmínky určují definiční obor. Exponenciála spolkne cokoliv, ale v jejím exponentu máme logaritmus, což vyžaduje, aby bylo cos(2x) kladné. Máme i druhou podmínku, zlomek očekává nenulový jmenovatel. Nejprve se podíváme na první podmínku. Je to nerovnice s goniometrickou funkcí, takže použijeme přístupy ze sekce Řešíme rovnice a nerovnice v části Extra. Začneme tím, že podmínka cos(y) > 0 má řešení

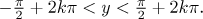
Teď dosadíme y = 2x a vyřešíme pro x.

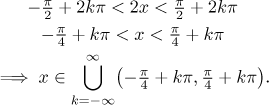
Druhá podmínka znamená, že sin(x) není nula, tj. x nemůže být kπ. Bohužel tyto body padnou přesně doprostřed intervalů výše, takže dostaneme tento škaredě vypadající definiční obor:

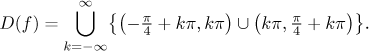
Teď potřebujeme najít limity ve všech krajních bodech intervalů této množiny. Je jich nekonečně mnoho, ale naštěstí je daná funkce 2π-periodická, což znamená, že stačí najít limity v koncových bodech jedné periody. Všimněte si, že jedna perioda zahrnuje dva sousední páry intervalů z onoho sjednocení, protože perioda funkce je 2π, zatímco perioda popisu definičního oboru je π. Pro výpočet použijeme například ty dva s k = 0 a k = 1. Protože daná funkce má tvar exponenciály, ušetříme čas tím, že nejprve najdeme limitu exponentu a teprve pak ji dáme do exponenciály.

Vidíme, že vlastně máme limitu f v 0, je to společná hodnota jednostranných limit 1. Analogicky spočítáme limity pro k = 1.

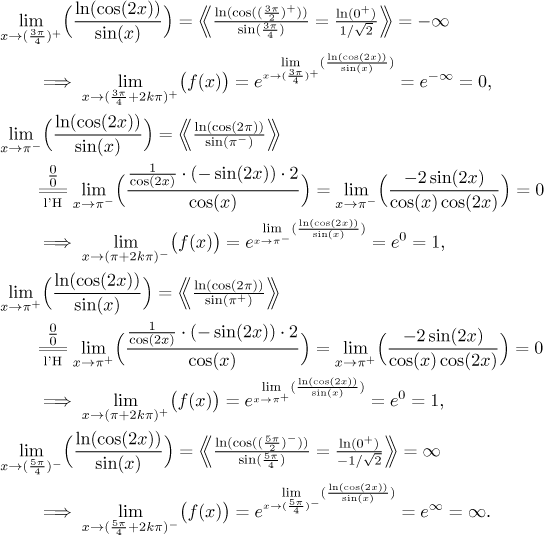
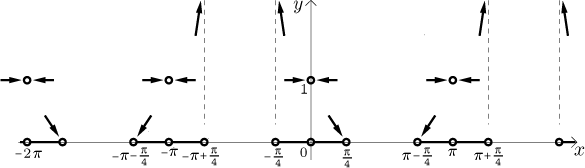
Teď můžeme načrtnout výsledek.

Další příklad
Zpět na Řešené příklady - Průběh funkce