Problem: Find the global extrema of

f (x) = x2 − 8|x − 1| + 8

on the interval I = [−1,6].

Solution: To find global extrema over a closed bounded interval we compare values of f at suspicious points. There are two kinds of candidates: the endpoints (here −1 and 6) and critical points of the given function.

There are two sorts of critical points: Points from the domain where the derivative does not exist and points where the derivative is zero. Thus we start by finding the derivative of the given function. We see that it includes absolute value, which means that we cannot find its derivative directly. First we have to get rid of the absolute value by rewriting the function as a split function.

We can find the derivative of such a function using the usual rules only on open intervals from its definition.

What about the derivative at 1? We can determine whether there is a derivative using one-sided derivatives (see Remark below), but in fact it is not needed here. We are only looking for suspicious points where extreme may happen and the point x = 1 is suspicious enough, we include it in the list of candidates (it does belong to our set I). Other candidates can be found by looking for zero points of this derivative.

The number x = 4 satisfies x > 1, so it lies in the region where the appropriate formula gives f ′ and it is a valid zero point of the derivative. Similarly, x = −4 is a valid zero point. However, we are interested in what is happening on the set I and −4 is not there, so we disregard it.

We have 4 candidates for global extrema: −1, 1, 4, 6. We compare the values:

f (−1) = −7,
f (1) = 9,
f (4) = 0,
f (6) = 4.

We see what the largest and smallest value is and conclude that max I ( f ) = f (1) = 9 and min I ( f ) = f (−1) = −7.

Remark: If we wanted to see whether there is a derivative at 1, the easiest way is to find one-sided derivatives at 1 using limits, see the appropriate theorem in section Derivative and limit in Theory - MVT. We would calculate

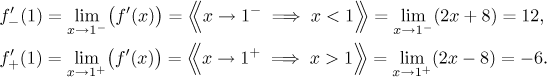
Since the one-sided derivatives do not agree, there is no derivative of f at 1.

Next problem
Back to Solved Problems - Applications