Problem: A beverage is to be sold in cans shaped as cylinder.
The volume of this cylinder must be
Solution: Your basic cylinder is given by two parameters, its height h and the radius of its base r. These will be our variables, we use centimeters a units. We were also told what is the "cost function" that should be optimized: It is the surface. The appropriate formula says that
We also have a constraint, a condition that must be satisfied. It says that
We can use this condition to eliminate one variable, here it will be probably easier to express h from this condition and substitute it into the formula for surface.
![]()
We want to minimize this function over the set of all reasonable values of
r, which in this case is the interval
To find a global minimum we compare values at suspicious points. Two suspicious points are endpoints of I, that is, 0 and infinity, but since they do not actually belong to I, we will use limit to find the value. Other suspicious points are the critical points of the function S. We find the derivative.
![]()
There are no points of I where this derivative would not exist, so the
only remaining source of suspicious points are zero points of this
derivative. The equation
![]()
As a positive number this belongs to I, so it qualifies as a
suspicious point. Now we substitute into S, the cubic root fits in
better if we write r 2 as
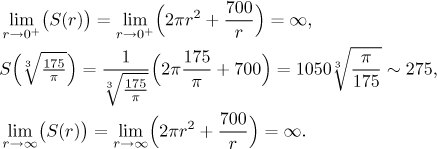
We see that the minimal surface is attained when r is the zero point of the derivative. Thus the optimal dimensions for the can are
![]()
We modified the formula for h so that it is easier to substitute r (as a cubic root) into it. Height is double the radius, that is, the optimal can has the same height as the diameter and looks a bit "squarish" (it looks like a square from the side and would fit tightly into a cube). By the way, nature often needs to optimize surface. For instance, given a certain volume of liquid, it has to spend energy on its surface, thus in nature liquid assumes shape with the least surface (if there are no other restrictions). This is the reason why in weightless environment water forms drops shaped like balls. If some magician forced water to form cylinders, our calculations shoved that the cylinder would be "squarish", not prolonged.
Back to our problem. How come beverages do not come in such optimal cans? The reason is that there are more considerations than just the surface. One important consideration is that you spend more material on the connections between bases and the sides, so it is smart to make those connections smaller. If we prolong a can while keeping its volume constant, we increase its surface, but its radius decreases and we save on those expensive edges. Another consideration concerns transportation. If we put cylinders with large radius into a box, we have to make the box large, since there will be a lot of room wasted between the cans. If cylinders are narrow, then there is less space wasted. This obviously fits with our real-life experience, we put more material into a jar if we use sand compared to large stones. Thus there are good reasons for making the cans narrower, there might also be other reasons (it might be easier to hold them and drink from them).