Problem: On a straight shoreline there is a tree and exactly opposite it, 100 m away in the sea, stands a lighthouse. A strong and thin spotlight on its top revolves at the rate of one revolution per 4 seconds, its light creating a running light spot on the shore. You stand on the shore 100 m from the tree. How fast does this spot move when it goes past you?

Solution: Here's how the situation looks like.

We need some mathematical description of this situation. The important things are the ray whose position is given uniquely by its direction and the light spot, whose position changes along the shore. Thus we introduce two variables as functions of time. One will be the position of the light spot x = x(t) along the shore, we need to choose the zero point and it seems that the logical choice is the tree, that is, exactly opposite the lighthouse. The direction is irrelevant due to symmetry, so we let x increase to the right where our position is and assume that the light also turns in this direction. The other variable will be the angle at which the spotlight shines measured with respect to the connecting line between the lighthouse and the tree.

This choice is reasonable for two reasons. First, it allows us to express important facts from our problem as derivatives, namely we know the rate of change of the angle and we are asked to provide the speed of the light spot, that is, the rate of change of its position. Thus we see that we need to relate two rates of change, which is another confirmation that our choice of variables was reasonable.

If we want to relate rates of change, that is, derivatives of two functions, we first have to relate the functions themselves. This is rather simple, from the right-angle triangle in the picture we have

Both sides of this equality are in fact functions of time, so we can differentiate them and obtain an equality again, we do not forget to use the chain rule on the right.

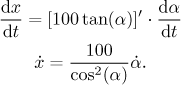
Of course, this equation only works for angles which make the light shine toward the shore, that is, for angles from the interval and its shifts by 2π.

The speed of rotation on the right is given by the fact that the light makes a whole circle, that is, the angle 2π, in 4 seconds, therefore it makes a quarter of a circle in one second. We get

Again, this only works for angles as above. Note that this formula behaves in a way that agrees with our common sense. The speed of the light spot is smallest exactly opposite the lighthouse (when the angle is zero) and the further we go from the tree, the faster the spot goes. It remains to find out the speed at the place where we stand. There the corresponding angle is π/4 and we get the answer.

This makes about 1131 km/h (or about 710 mph), which is pretty fast (faster than sound, by the way).

Next problem
Back to Solved Problems - Applications