Problem: Find the Taylor polynomial of degree 3 and of degree n with center a = 0 for the function

f (x) = ln(1+2x).

Solution: The Taylor polynomial at a of degree 3 is given by the formula

So we need to calculate the first three derivatives and then substitute a = 1 into them. It is a good idea to be organized, I do it like this: First I put all derivatives in one column, then I do the substitutions in another column.

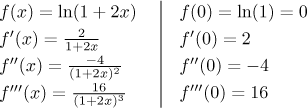
We substitute this and a into the general formula and obtain

Now we will look at the problem of guessing the Taylor polynomial of degree n. For simple problems it might be possible to guess correctly from the Taylor polynomial of degree 3 or 4, but here it might be tricky, so we will show a procedure that is quite reliable. The main trick is to look not at the numbers in the right column above but at the left column, identifying individual factors that keep appearing at each step of the derivative. What happens when we differentiate? We will redo the above derivatives to see the process.

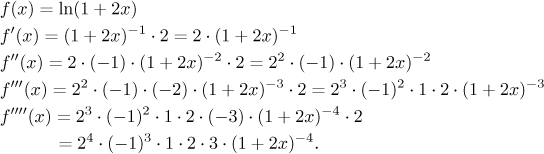
We should now see the pattern. With each derivative we get an extra 2, an extra (−1) and then an increasing string of multiplied numbers, giving rise to a factorial. We also notice that we get the 2 exactly as many times as is the degree of the derivative, but the power at (−1) and the factorial are smaller by 1. The power at (1+2x) agrees with the degree of derivative (apart from the minus). We are ready to make a general conjecture about the k-th derivative.

We check that it agrees with the first three derivatives we calculated at the beginning, so it seems reasonable that it is correct, just to be on the safe side we will prove it by mathematical induction. For k = 1 it works, now we pass from k to k + 1.

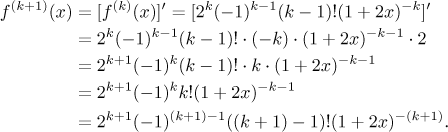
This proves that our guess concerning the k-th derivative was correct, so we can substitute 0 into it and then use it in the general formula for the Taylor polynomial of degree n, we use the summation form first to simplify calculations. Recall that the 0-th derivative is given by a different formula, so we have to separate it from the rest when substituting.

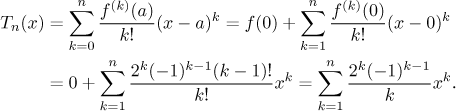
Check that the first three terms of this general formula agree with our T₃ above.

Remark: There is an easier way to get T_n. One of the classical results that can be found in pretty much every textbook dealing with Taylor polynomials is the Taylor polynomial for the function ln(1+y).

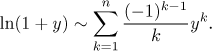
If we substitute in y = 2x, we get exactly the result we obtained with direct calculation.

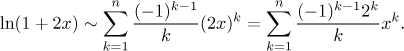
Remark: This is a nice example that one has to be careful when approximating using Taylor polynomials. If we use this approximation at x = 1/4, then it will be good, and the quality will improve with rising degree of Taylor polynomial. However, it can be also proved that if we put x = 1 into these polynomials, then they will not approximate ln(3) at all, in fact their values start oscillating wildly with increasing degree. For more insight see Taylor series in Series - Theory - Series of functions.

Next problem
Back to Solved Problems - Applications