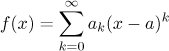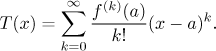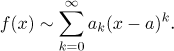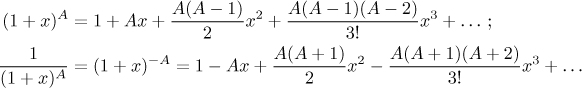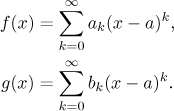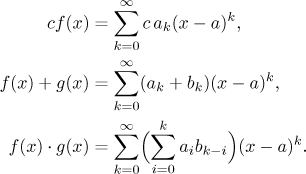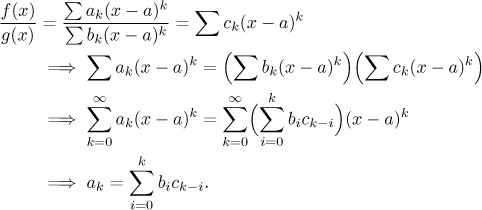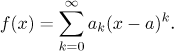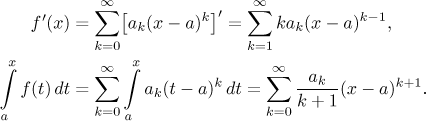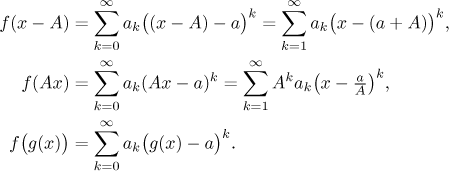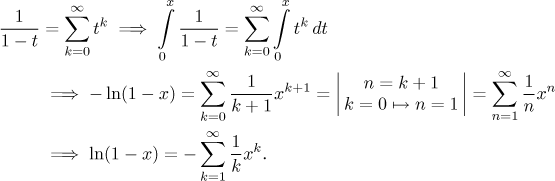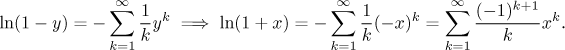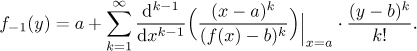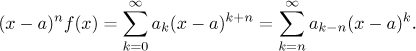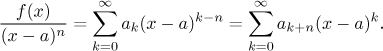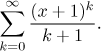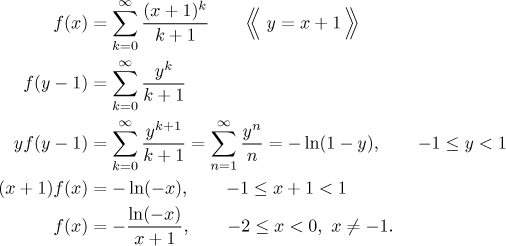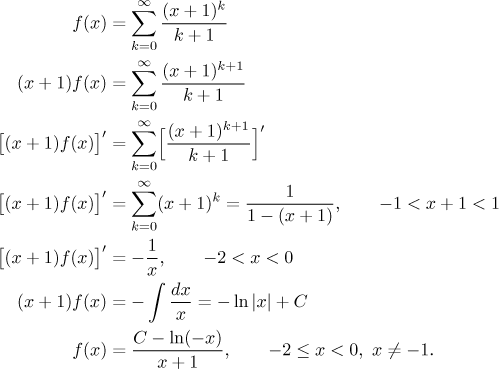Taylor series, expanding functions, summing up series
Here we address the main question. We have a function f and a number
a and we would like to express this function as a sum of a power
series with center a. We
start with some theory and then look at expanding using
properties. At the end we address the reverse
process, to a given series we try to find its
sum.
As
we outlined in general in the section
Systems of functions, there
are two questions to be answered: What functions can be expressed in this
way and how do we find the series for them. And the first question is indeed
hard, we will just give a partial answer later. We start by a definition.
Definition.
Let f be a function and a some point from the interior of
its domain.
We say that we expanded the function f in a power
series (at a) if we find some power series such that
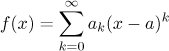
on some neighborhood of a.
This power series is then called an expansion of f.
From the results in the
previous section it follows
that every function that can be expanded in this way must have derivatives of
all orders at a. This tells us that there is no point in trying to
expand other functions. It also says that when we talk about expanding, we have
all these derivatives available.
The starting point of our investigation is the Corollary at the end of the
previous section. Assume that
we have a function that can be expressed by a series at a. If we
substitute this center a into the formula for the n-th
derivative, we immediately get the following.
Theorem (uniqueness of expansion).
Let f be a function that can be expanded in a power series
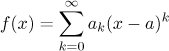
on some neighborhood of a. Then for every k, the coefficients
ak necessarily satisfy
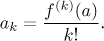
In other words, there is only one way to expand a function into a power
series (if it can be done at all). This unique power series deserves a name.
Definition.
Let f be a function and a some point from the interior of
its domain. Assume that f has derivatives of all orders at a.
Then we define its Taylor series at a by the formula
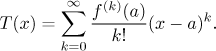
The formula for coefficients is the same as in the case of
Taylor polynomial,
so this is really something like an "infinite Taylor polynomial".
Note that the theorem above was an implication. This means that once we have
a function expanded into a power series, then this series is necessarily the
Taylor series. However, if we take a function with all derivatives at
a and construct the Taylor series according to the above formula,
then there is no guarantee that this series will be convergent also
somewhere else than at a, and even if it converges, there is no
guarantee that it actually converges to the original function f.
For instance, in
this note we show an example of a
function that is "nice" by most standards (it has derivatives of all orders
everywhere), its Taylor series converges to its sum uniformly on the whole
real line, yet the sum of this Taylor series is equal to the original
function only at one point, the center of the series (where it actually has
to work for any function and series, so it has no choice). This situation
where we have trouble with getting the series to go to the right place
appears often when we work with systems of functions, and it inspires the
following notation.
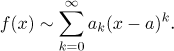
The tilde means that the series on the right was obtained from f
using the above formulas (it is the Taylor series for f ),
but it also means that the process of creating this Taylor series is purely
formal, since at this moment we have no information whether the sum of this
series actually has anything in common with f.
Obviously, our aim is to change this tilde into equality, that is, we would
like to see that the Taylor series on the right actually converges to
f at least somewhere (apart from a, where the convergence is
automatic). How do we recognize this? By definition we should take the
partial sums TN of T and check whether they
converge to f.
Equivalently, we would like to find out how the difference
| f − TN|
behaves, hoping that it would go to zero as N goes to infinity.
However, this is actually something that we already saw before, since
TN are exactly
Taylor polynomials
(see Derivatives - Theory - Applications),
so we know quite a bit about this difference. In particular, we have the
Lagrange
estimate of it. Thus we can restate the question like this:
Assume that f has derivatives of all orders on some neighborhood
U of a. Let x be such that the closed interval I
with endpoints a and x lies in U. We want to know when
it is true that
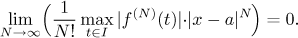
Note that in this formula, x is fixed and thus
x − a is a constant. When we recall
that
cN/N! tends to zero at
infinity, we see that all depends on how quickly the maximum grows with
N. If it does not grow at all or grows very slowly, then the Lagrange
estimate of the error goes to zero. Thus we get the following.
Theorem.
Let f be a function such that it has derivatives of all orders on
some neighborhood U of a point a. Let T be its Taylor
series at a.
If there is a constant M such that
| f (k)(t)| ≤ Mk
for all positive integers k and all t from U, then T
converges (uniformly) to f on U.
Thus we get one group of functions whose Taylor series is actually equal to
them, namely functions with uniformly bounded derivatives. However,
this condition is too restrictive, there are also other functions whose
Taylor series converge to where they should. Finding the right
characterization is a hard task, definitely beyond the scope of Math Tutor,
and we leave it to professional mathematicians.
There are some functions for which we can easily find their expansions.
By uniqueness of expansion, every power series is its own Taylor series
(with the same center). Expanding with a different center than "their own"
is not so simple any more, but it can still be done in case of "finite"
series, that is, in case of polynomials. We just need to create the
right center. For instance, if we want to find the Taylor series for
x2 with center a = 1,
we simply do
x2 = [(x − 1) + 1]2 = (x − 1)2 + 2(x − 1) + 1.
The latter is a power series with center 1 (its coefficients are zero for
k > 2), and so it is the desired Taylor
series. (We would get the same series if we used the formula from the
definition, of course.) Trying this trick for an infinite series would
not be nice any more.
Now we now look at six famous expansions that are the basis of most
other expansions.
Theorem.
The following expansions are true on the indicated sets.

As these formulas suggest, the choice
a = 0
for the center is very popular. In fact, it is so popular that some people use
the traditional name McLaurin series for Taylor series with this center.
However, it is not universal and you find it especially in older texts.
In all six cases we find the formula for Taylor polynomials easily from
definition. How about their convergence? The second and third formula is clear,
convergence follows from the previous theorem (sine and cosine have all
derivatives bounded by 1 everywhere).
For the exponential we can use this theorem as well, but we cannot do it
globally, since the exponential is bounded only on bounded sets.
However, this is no problem. If we take any real number x, we can
always consider for instance the open neighborhood
U2|x|(0). This is a bounded set and
all derivatives of ex are therefore uniformly
bounded on it, so by the above theorem, the Taylor series converges to the
exponential there; in particular it converges to the exponential at x,
since x belongs to this neighborhood. For the sake of completeness we
include a direct proof using the Lagrange estimate, see
this note.
The expansion for logarithm can be actually obtained in several ways, we
will return to it also below; concerning its convergence, the interval we
stated is clearly the largest one can hope for, since in the
previous section we proved that
this interval is exactly the region of convergence of this Taylor series.
Thus it remains to show that the sum of the series on this region is exactly
ln(x). However, here one cannot use the above Theorem, since
derivatives are not uniformly bounded. This case is therefore far trickier,
for more details see
this note.
The fifth formula is just the
geometric series, so there
is nothing new about it.
Probably the most interesting of the six is the last formula, also called
the binomial series or binomial expansion. It is true for all
c and A, which in particular shows, that the binomial numbers
can be also defined for a general number A. It is done by the second
formula with the understanding that when k = 0, we get 1.
As an example we show how the series looks like when c = 1,
which is a frequently used form. We also show a special formula for "minus
A", it is sometimes useful when working with reciprocals. Both work
for |x| < 1.
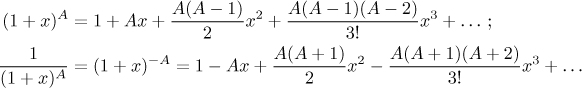
Note also that if A is a natural number then by definition, for
k > A all the coefficients are zero.
Thus the sum is finite, it always converges and it is in fact the familiar
binomial formula that we know from high-school.
One reason why these formulas are important is this: We rarely expand
functions by definition, the way we did it above. In most cases we use
various tricks to somehow get new expansions out of those that we already
know. The above six are the starting point for most such calculations. The
tricks are coming up just now.
Expansion and operations
In order to get expansions of new functions from known expansions we use
properties known to work for power series. The theorem on
algebraic operations from the
previous section gives this handy fact.
Theorem.
Assume that we have these expansions on some neighborhood of
a.
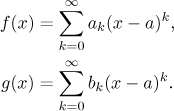
Then on this neighborhood also
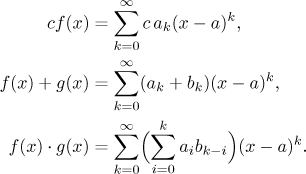
How about the division f /g? Obviously it is
enough to know how to expand the function 1/f (assuming
that f (a) ≠ 0).
Theorem.
Assume a function f can be expanded in a Taylor series at
a and that
f (a) ≠ 0.
Then also the function
1/f can be expanded in a Taylor series at a and
this series has a positive radius of convergence.
This theorem does not offer any formula for the new series - and with a good
reason, there is no reasonable way to specify it. In practice we use the
method of undetermined coefficients. We can actually apply it
directly to f /g
and take 1/f as the special case. Assume that both
f and g are expanded into their Taylor series at a and
that g(a) ≠ 0.
By the above theorem, also their ratio can be
expanded in a Taylor series with yet unknown coefficients
ck.
We can write
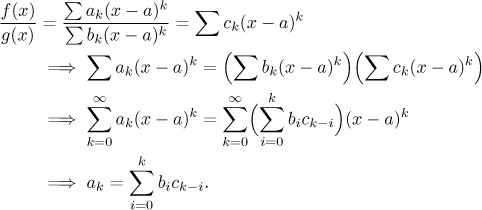
The resulting system of infinitely many linear equations with infinitely
many unknown
ck
is usually impossible to solve explicitly, but it allows us to calculate as
many coefficients
ck
as we want, which is very useful when we want to approximate
f /g
using just a finite part of the Taylor series.
For an example we refer to Solved problems, namely
this problem (it is unusually
nice but illustrates the idea well) and
this problem
(it is more typical).
We also often relate functions to other functions using derivative or
integral. Then we can use
this theorem from the previous
section.
Theorem.
Assume that we have the following expansion on some neighborhood of
a.
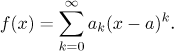
Then on this neighborhood also
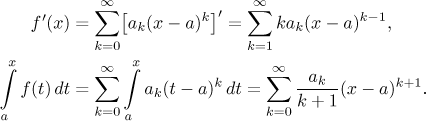
One can also use indefinite integral in the second statement, but then it is
necessary to work out the right constant. We will show an example below.
Finally, there are other operations that can help in expanding new functions.
Theorem (substitution in series).
Assume that we have the following expansion on some neighborhood of
a.
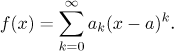
Then also
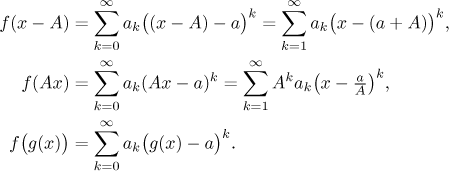
The first statement holds for any A and the radius of convergence of
the new series is the same as the original one, but its center (and region
of convergence) are shifted accordingly.
The second statement holds for all non-zero A and the radius of
convergence of the new series is
Rf /|A|.
The third statement is a bit shaky, since the outcome is a power
series only for very special g. The region of convergence then has to
be investigated individually.
In fact, in the first two statements we actually know even the region of
convergence of the new series. In the first statement, the new region is just
the original one but shifted. The region of convergence in the second case
can be obtained by shrinking the original one, for A negative one
also has to flip it around a. That is, if the original series
converges at the right endpoint, then the new one also converges at the
right endpoint for A > 0 and it converges
at the left endpoint for A < 0. It is all
actually just a common sense and understanding substitution well.
Example: We will deduce the expansion for
f (x) = ln(1 − x) at
a = 0.
The key to this expansion is the observation that
f ′(x) = −1/(1 − x)
and this is exactly the sum
of the
geometric series that
everybody knows. So we start by taking the formula for geometric series (we
use variable t) and then we integrate both sides from 0 to
x
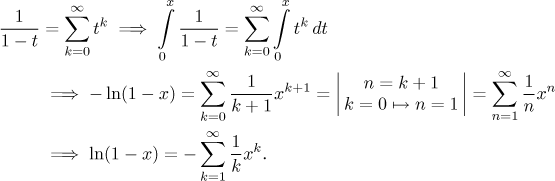
This series is often used for logarithm.
The original series converges for t satisfying
−1 < t < 1, so the new one
also converges at least on this set and its radius of convergence must
stay the same (that is, 1). However, we may have gained convergence at some
endpoints. When we put in
x = −1
and
x = 1
and use suitable tests, we find that the region of convergence of this
series is
[−1,1).
How do we know that the sum of this series at
x = −1
is equal to
ln(2)?
One possible argument is to use continuity, see
Abel's convergence theorem
in the previous section. Thus we have expansion valid on
[−1,1).
If we write this result using y and then use the substitution
y = −x,
we get
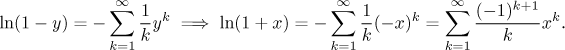
The original series converges for y satisfying
−1 ≤ y < 1,
so when we substitute
-x
for y, we get the region of convergence
(−1,1] for the new series.
On the other hand, if we substitute
y = 1 − x,
then we get exactly the series for
ln(x)
that we had in the above
Theorem.
It is perhaps surprising in view of difficulties we had with finding series
for
1/f
that there is in fact an explicit way to expand inverse function.
Theorem (Lagrange inversion formula).
Assume that a function f can be expanded in a series on some
neighborhood of a point a. Assume further that
f ′(a)
is not zero. Denote
b = f (a).
Then there is a neighborhood of a on which the function f is
invertible and a neighborhood of b on which this inverse
f−1
can be expanded in a power series. Moreover, this series can be found as
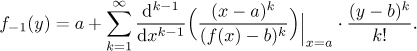
We conclude this part with yet another useful statement.
Theorem.
Assume that we have the following expansion on some neighborhood of
a.
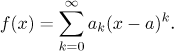
Then on this neighborhood we also have the following expansions.
(i) For any positive integer n,
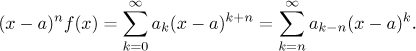
(ii) If f has a root of multiplicity n at a, then
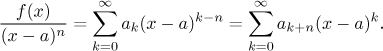
The second statement makes sense for the following reason. If a is a
root of multiplicity n for f, then the first
n − 1 derivatives of f at a are
zero
(see this note).
Therefore also the first
n − 1
coefficients of the Taylor series are zero, which means that in fact in the
series for f the indexing starts at n, not at 0. This explains
why after shifting the index we get the second formula.
For more examples of using the above properties to expand functions see
Methods Survey
and
Solved Problems - Series of
functions.
We conclude this part on properties of Taylor series with a fact that one could
already guess from the six expansions above.
Fact.
Let f be a function that has Taylor series with center at
a = 0, let
ak be its coefficients.
If f is odd, then
ak = 0 for all even k.
If f is even, then
ak = 0 for all odd k.
Summing up series
We mentioned several times that summing up series can be rather difficult.
The above tricks for expanding a function can be also used to sum up a power
series (assuming that we are lucky). The basic idea is to change the given
series into one that we already know by applying transformations from the
above theorems to it while keeping track of what it does with its sum. It is
best explained on an example.
Example: Find the sum of
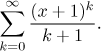
Is there a series that looks like this? There is a series that has terms
yk/k,
we can almost get there by denoting
y = x + 1.
It remains to fix the power so that it agrees with the number in the
denominator, but that is not a problem. Here we go.
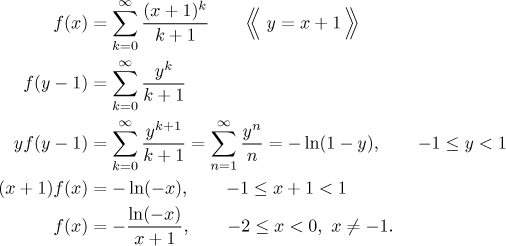
What about the value x = −1? This is simple, we
just put it into the given series and find that
f (−1) = 0.
We can also try another approach. Often we need to get rid of extra k
in a series. In our series we have extra
k + 1
in the denominator, so we would appreciate if
k + 1
appeared also in the numerator. There is a way to get k in the
numerator, namely by taking derivative of a series. We need
k + 1,
so before differentiating we need to create
(x + 1)k + 1
there. Once there is no division by k + 1,
we use
geometric series.
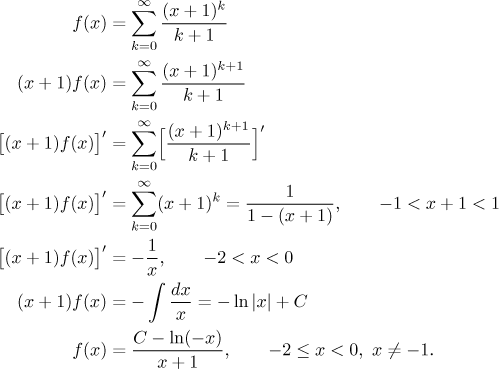
It remains to fix the right C. The easiest way it to simply put some
nice x into the last equality. Since on the left we substitute
into f, that is, into the given series, we do not have much choice.
The only value that we can really put in this series is
x = −1, but unfortunately, that is the one
value we are not allowed in the last line. What can we do?
It would seem that we could fix this problem by using the second last line.
Looking closer we see this is not true. Note that if
x = −1, then on the second line we multiply by
zero, which is not allowed in the equation. Thus for this value all
subsequent equalities are suspect. Fortunately for us, we can look still
closer. What do we have on that second last line? We have one function on
the left and another on the right and we know for sure that they are equal
for all x from a certain interval except one point in its middle.
Since these two functions are continuous, we also must have equality at this
particular point. We are saved, we substitute −1 in the second last line and
learn that C = 0. Since we used integration
that influences endpoints, we should now check on convergence at −2 and at 0
and we would get the same conclusion as above.
Fourier series
Back to Theory -
Series of functions