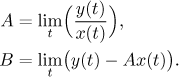
Uvažujme parametrickou křivku danou rovnicemi
x = x(t),
y = y(t) pro t z nějakého
intervalu I.
Předpokládejme, že funkce
Nejprve zkusíme zjistit co nejvíce z popisu, který máme, a pak použijeme přístup přes funkce. Většina bude selský rozum; nejdůležitější věc, kterou je třeba mít na paměti, je to, že budeme míchat "časový" a prostorový pohled a přesouvat informaci z jednoho systému do druhého. Vědět, kde se v každé dané fázi výpočtu nacházíte, je zásadní a také v zásadě postačující pro úspěšné zvládnutí úkolu. Abychom naše úvahy ilustrovali, budeme simultánně s výkladem pracovat na příkladě.
Příklad: Zkoumejte parametrickou křivku
x = (t − 1)2,
y = t3,
t ≥ 0.
Teorie:
Co se dá z popisu říci? První důležitá informace je o koncích. Jestliže
interval I zahrnuje některé ze svých koncových bodů, pak dosazením
takového času do x a y zjistíme, kde dráha začíná nebo končí.
Pokud některý koncový bod zahrnut není, pak najdeme příslušnou jednostrannou
limitu x a y vzhledem k t. Interpretace těchto výsledků
je docela zajímavá. Jestliže jsou obě limity vlastní, pak křivka prostě jde k
bodu, který jsme tak dostali. Jestliže jsou obě limity nevlastní, pak křivka
jde do jednoho z rohů. Selský rozum by měl napovědět, například jestliže
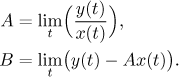
Zajímavý případ je, když je jedna limita vlastní a druhá nevlastní. Pak totiž dostaneme vodorovné a svislé asymptoty, jak ukazujeme na tomto obrázku:
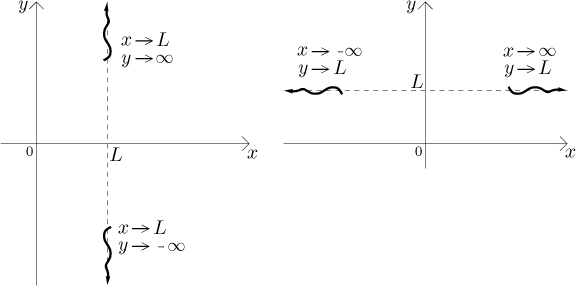
Další tradiční informace jsou průniky s osami. Průniky s osou x jsou
dány časy t splňujícími
Zpět k našemu Příkladu: Interval
![]()
Křivka tedy začíná v bodě
Průsečíky: Průsečík s osou
y je dán rovnicí
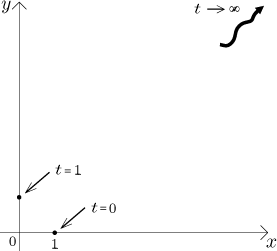
Teorie: Teď se podíváme po dalších bodech křivky. Samozřejmě chceme body "důležité", kde se něco mění. Začneme s x. Tato proměnná zaznamenává pohyb ve vodorovném směru, takže když x roste, pokybuje se křivka doprava. Jestliže x klesá, tak se křivka pohybuje zprava doleva. Lokální extrémy x jako funkce jsou otočné body pro dráhu. Další přirozený krok je tedy zkoumat monotonii funkce x jako samotné. Namísto růstu/klesání ale budeme znaménka derivace interpretovat jako pohyb doleva/doprava po křivce. Časy t, které dávají lokální extrémy x, dají po dosazení do x a y body obratu.
Všimněte si, že tato informace ještě není dostatečná na to, aby dala dobrou představu o dráze. Na následujícím obrázku mají obě křivky stejné otočné body vzhledem k x a identické pravolevé směry, ale jsou dost rozdílné.
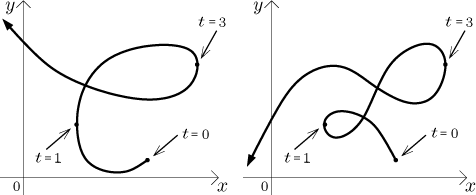
Abychom dostali lepší informaci, podíváme se podobně na funkci y, která dává svislý pohyb, takže když ji prozkoumáme jako nezávislou funkci, tak časy t odpovídající lokálním extrémům ukážou, kde se dráha mění mezi směry nahoru a dolů.
Zpět k našemu Příkladu: Najdeme
![]() (t) = 2(t − 1),
(t) = 2(t − 1),
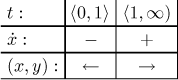
Čas obrátky
Máme také
![]() (t) = 3t2,
(t) = 3t2,

Lepší představu o směru dráhy dostaneme, když tyto samostatné tendence zkombinujeme.

Teď známe základní směry a můžeme nakreslit hrubý obrázek.
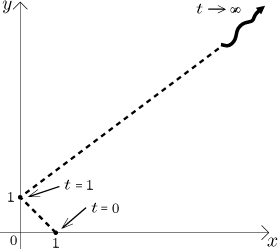
Všimněte si zajímavé věci. Když se díváme na části křivky jako na grafy dané
nějakým
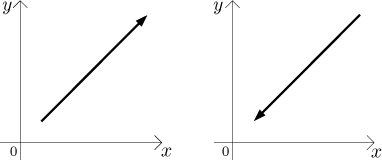
V té tabulce nahoře to odpovídá tomu, že odmažeme šipky, pak dostáváme jen
rostoucí a klesající tendence grafu. Všimněte si, že poslední obrázek
ukazuje, že rostoucí graf dostaneme pro kombinace + + a − −
znamének ![]()
![]() .
.![]() /
/![]()
Zatím jsme ještě opravdu nepotřebovali pohled prostřednictvím funkcí. Jak jsme právě viděli, můžeme zkoumat pohyb pravolevý a nahoru/dolů, nebo uvažujeme funkci y popisující křivku a zkoumáme její znaménko, nakonec dostaneme pro křivku stejné tendence. Teď bychom nicméně rádi dále zpřesnili obrázek, což volá po konvexitě a tam už potřebujeme přístup skrz funkce.
Připomeňme vzorec pro druhou prostorovou derivaci:
![]()
Zpět k našemu Příkladu: V našem případě dostaneme
![]()
Jaké jsou dělící časy pro konvexitu? Z čitatele máme

Čas
![]()
Teď bychom tedy měli být schopni křivku nakreslit. Protože o časech po
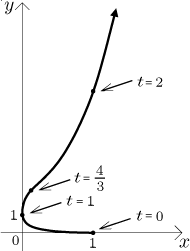
Ještě jeden trik, který se dá zkusit: Když je čas opravdu velký, pak je
x přibližně t2. Odtud můžeme vyjádřit t a
dosadit do y, čímž se dozvíme, že pro opravdu velké časy křivka vypadá
jako graf funkce