Derivace parametrické funkce

Uvažujme parametrickou křivku danou
x = f (t),
y = g(t)   pro t z intervalu I, kde f a g jsou spojité funkce.

Uvažujme také bod (x0,y0), který leží na této křivce, tedy x0 = f (t0) a y0 = g(t0) pro nějaký konkrétní čas t0. S trochou štěstí existuje okolí tohoto bodu, na kterém lze křivku popsat pomocí funkce y = y(x). V sekci Parametrické funkce v části Funkce - Teorie máme větu, která má dostačující podmínku pro to, aby se to stalo. Tato podmínka je f ′(t0) ≠ 0.

Tato podmínka znamená, že f je buď rostoucí nebo klesající v t0, takže se v tomto čase křivka pohybuje doleva nebo doprava při průchodu daným bodem. Věta tvrdí, že tam můžeme křivku popsat jako funkci. Můžeme si představit, že funkce f je vlastně prostá okolo daného času, můžeme tedy najít její inverzní funkci t = f−1(x) a použít k eliminaci t z rovnic. Dostaneme

y(x) = g( f−1(x)),

viz Parametrické funkce v části Funkce - Teorie. Pokud budeme předpokládat, že f a g jsou diferencovatelné v t0, pak je i celá funkce napravo diferencovatelná, proto také y(x) a dokonce máme vzorec pro derivaci. Ten bude ještě zajímavější, když použijeme vzorec pro derivaci inverzní funkce (viz Derivace a operace v části Teorie - Úvod). Dostaneme následující tvrzení:

Věta.
Uvažujme parametrickou křivku danou
x = f (t),
y = g(t)   pro t z intervalu I.
Předpokládejme, že f a g jsou diferencovatelné v nějakém t0 z vnitřku I a že f ′(t0) ≠ 0. Pak existuje okolí t0, na kterém se dá odpovídající část křivky vyjádřit pomocí funkce y = y(x).
Tato funkce je navíc diferencovatelná v x0 = f (t0) a máme

Použili jsme funkce f a g namísto tradičního zápisu typu x = x(t), x = x(t) pro popis souřadnic. Pokud bychom šli tradičním způsobem, dostali bychom věci jako t = x−1(x), kde to první x je funkce a to druhé proměnná, což je pro začátečníka docela zmatek. Když už teď ale máme výsledek, je zajímavé jej přepsat tradičním způsobem, připomeňme, že tečka znamená derivaci podle času.

Bude to ještě zajímavější, když použijeme Leibnizovo značení.

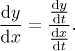
Teď to vypadá jako obyčejné krácení, takže Leibnizovo značení zase způsobí, že věci vypadají přirozeně.

Všimněte si vzájemné provázanosti časového a prostorového uvažování. Na tuto křivku se můžeme dívat jako na objekt v rovině nebo jako na záznam pohybu v čase. Když chceme derivaci vzhledem k souřadnici x v určitém bodě v prostoru, tak ji vzorec dává do souvislosti s časovými derivacemi, do nichž samozřejmě dosazujeme čas, jmenovitě ten, ve který dojdeme do daného bodu. Je to zcela přirozené, ale může to poplést, když si nedáte pozor. Při zkoumání parametrické křivky je třeba dávat pozor na to, co je prostorové a co je časové. Pro bližší pohled na toto pravidlo viz příští sekce.

Když už máme vzorec pro první derivaci, můžeme derivovat podruhé a dostaneme následující.

Věta.
Uvažujme parametrickou křivku jako v předchozí větě se všemi vlastnostmi tam zmíněnými. Předpokládejme navíc, že f a g jsou dvakrát diferencovatelné v t0. Pak je funkce y = y(x) také dvakrát diferencovatelná v x0 = f (t0) a máme

Pokud použijeme tradiční značení pro parametrické křivky, dostaneme

Jak jsme tento výsledek dostali?

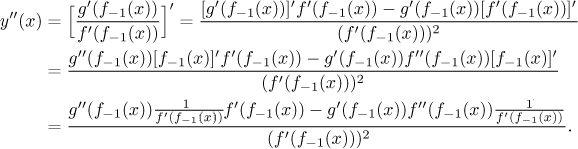
Pak jen dosadíme x0, použijeme f−1(x0) = t0 a je to hotovo.

Příklad: Uvažujme parametrickou křivku
x = t⋅et,
y = t3 + 6t   pro t ≥ −1.
Dokažte, že ji na okolí (e,7) můžeme vyjádřit jako funkci a najděte její derivaci.

Řešení: Čas, který odpovídá danému bodu, je t0 = 1. Vidíme, že (1) = 2e, což není nula a existence funkce y = y(x) na nějakém okolí (e,7) je dokázána.

Podle věty také máme

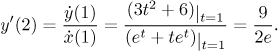
Přepis parametrické křivky na funkci

Už víme, jak derivovat lokální prostorový popis, teď se vrátíme k problému rozkladu dané křivky na části popsatelné funkcemi. Víme, že změna parametrických rovnic na funkci se dělá eliminací, na což potřebujeme, aby byla funkce x(t) prostá. Jeden snadný způsob, jak rozpoznat intervaly prostoty, je pomocí derivací.

Předpokládejme, že dokážeme rozdělit interval I na podintervaly takové, že na každém z nich derivace (t) existuje a je nenulová se stejným znaménkem. Pak je na každém z těchto intervalů derivace buď jen kladná nebo jen záporná, proto tam musí být funkce x prostá (viz Derivace a monotonie v části Teorie - Věta o střední hodnotě). Části křivky, které odpovídají těmto částečným intervalům, jsou proto přesně ty kousky, které jde (alespoň teoreticky) vyjádřit jako funkce.

Poznamenejme, že znaménko derivace (t) ještě nese další informaci, velice užitečnou při zkoumání křivky. Když (t) > 0, tak jde křivka doprava; když (t)  <  0, pak jde křivka doleva Ale to už se dostáváme k tématu kreslení křivky, což se probírá v sekci příští sekci.

Pro přehled a příklad parametrické křivky viz Parametrické funkce v Přehledu metod, příklad je také v Řešených příkladech - Parametrické funkce.

Život brouka

Teď se vrátíme, kde jsme začali. Hlavní myšlenka této sekce byla zapomenout na pohyb a redukovat parametrické křivky na obrázky a funkce. To se nám docela dařilo, dokonce se v příští sekci dozvíme, jak je kreslit. Teď toto téma ale opustíme a zeptáme se, jaké další informace se dají získat z parametrické křivky.

Vzhledem k tomu, že parametrická křivka je záznam pohybu, nabízí se otázka na okamžitou rychlost v libovolném daném bodě. Na to máme vzorec.

Jak jsme to dostali? Předpokládejme, že v čase t je brouk na určitém místě a pak se posune o čas dt. V prostoru to znamená posun o dx a dy, ale protože x a y jsou funkce t, dostaneme transformační vzorce

dx = ⋅dt,     dy = ⋅dt.

(Viz Leibnizovo značení v části Teorie - Úvod.) Protože jsme se posunuli o nekonečně krátký čas, tak se křivka ještě nestačila zatočit a můžeme ji považovat za přímku.

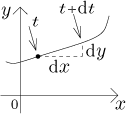
Proto se změna ds pozice s dá spočítat pomocí Pythagorova pravidla:

Když tohle vydělíme dt, dostaneme žádanou rovnost, protože rychlost je právě časová derivace pozice.

Dá se zjistit víc, například se dá spočítat délka uražené dráhy, ale to už vyžaduje integrování; odkazujeme na Délku křivky v části Integrály - Teorie - Aplikace. V sekci Obsah v části Integrály - Teorie - Aplikace se dozvíte, jak počítat plochu oblasti dané parametrickou křivkou, jsou tam také nějaké věci o těžišti.

Náčrt parametrických funkcí
Zpět na Teorie - Implicitní a parametrické funkce