Implicit functions and implicit differentiation

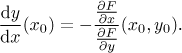
We start with some theory which is a bit beyond what we know so far (at least officially, namely we need to use functions of more variables), then we will look at practical approach.

Consider an equation F(x,y) = c and a point (x₀,y₀) that satisfies this equation, that is, a point that lies in the set described by this equation. With a bit of luck, there is a neighborhood of this point on which the set is actually a curve that can be described using a function y = y(x). In the section Implicit functions in Functions - Theory we have the Implicit function theorem which has a sufficient condition for this happening. It turns out that this condition is already strong enough to also guarantee differentiability of y(x) at the given point and the theorem even tells us how to find this derivative.

Theorem (Implicit function theorem).
Consider an equation F(x,y) = c. Let a point (x₀,y₀) satisfy this equation. If

then there exists a neighborhood U of x₀ and a function y = y(x) on this neighborhood such that y(x₀) = y₀ and F(x,y(x)) = c for all x from U.

Moreover, this function is differentiable at x₀ and

We used the Leibniz notation, since it makes clear with respect to which variable we differentiate. Nice as this rule is, we usually do not use it literally; rather, we repeat the procedure by which we obtain it.

The proof of this rule is quite simple. We take the original equation F(x,y) = c, assume that y is actually a function of x and differentiate both sides. If the original expressions are equal, then the derivatives must also be equal. When differentiating on the left, we should use the chain rule (we compose the function F with the function y(x)), in this case we need a generalization of the chain rule for functions of more variables.

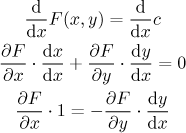
From the last equality we get the formula in the theorem. The trick of differentiating the equation and then solving for the derivative of y is called implicit differentiation and it is the easiest way to get the derivative of an implicit function.

Example: In Implicit functions in Functions - Theory we proved that the equation y³ + 1 = xy defines an implicit function y(x) on some neighborhood of the point (2,1). Find the tangent line to its graph at this point.

Solution: To get the tangent line we need a point - which we have - and its slope, namely we need y′ at x₀ = 2. To find this derivative we use implicit differentiation. We will differentiate both sides of the given equation, keeping in mind that y is actually a function of x. We will do it slowly with all details to explain what is happening.

[(y(x))³ + 1]′ = [x⋅y(x)]′
3(y(x))²⋅[y(x)]′ = [x]′⋅y(x) + x⋅[y(x)]′
3(y(x))²⋅y′(x) = y(x) + x⋅y′(x)

We obtained an equation that features y′(x), so we can solve it for this derivative. However, then we would need derivative at a particular point, so it may be easier to substitute right away.

3(y(2))²⋅y′(2) = y(2) + 2y′(2).

How much is y(2)? Our implicit function passes through the point (2,1), so y(2) = 1, hence

3⋅1²⋅y′(2) = 1 + 2y′(2).

From this we get y′(2) = 1 and we are ready to write the tangent line:

y = 1⋅(x − 2) + 1,     y = x − 1.

Remark: An experienced student could save some writing by not putting the (x) next to y in the equation, one can differentiate the equation as originally written and keep in mind that y is a function of x, obtaining the same result, for instance this line:

3y²y′ = y + xy′.

Instead of substituting x = 2 one can solve this equation for the derivative and obtain

This expression can be used to find derivative at all points from the neighborhood where this y(x) describes the given curve (note that we need to know both coordinates of such a point to be able to use this formula for y′, as it features both x and y = y(x)).

If we differentiate the equation that we obtained once more, we get the second derivative.

[3y²y′]′ = [y + xy′]′
[3y²]′y′ + 3y²[y′]′ = [y]′ + [x]′y′ + x[y′]′
6yy′y′ + 3y²y′′ = y′ + y′ + xy′′
6y(y′)² + 3y²y′′  = 2y′ + xy′′

From this we get

Similarly we can find higher order derivatives.

For a review and an example of implicit differentiation see Implicit differentiation in Methods Survey.

Derivative of parametric functions
Back to Theory - Implicit and parametric functions