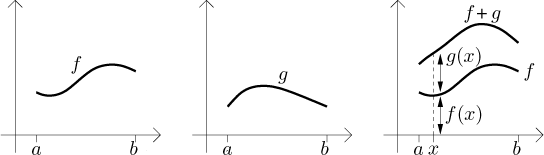
Uvažujme dvě funkce f a g definované na uzavřeném intervalu ⟨a,b⟩. Protože určitý integrál je spojen s obsahem a my zde neděláme důkaz, spíše jen intuitivní ospravedlnění, můžeme si dovolit předpokládat, že obě funkce jsou kladné. Nejprve si pro jistotu připomeneme, jak se dělá graf funkce f + g. V každém bodě x se nejprve posuneme nahoru o hodnotu f (x) a pak jdeme nahoru ještě jednou, tentokráte o g(x):

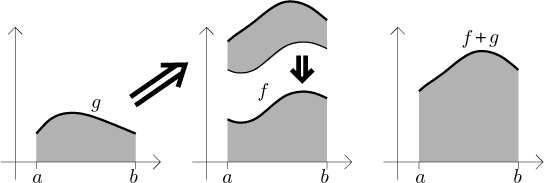
Teď bychom měli najít nějaký vztah mezi výslednou oblastí a oblastmi pod grafy samotných funkcí f a g. Podívejme se na graf g:

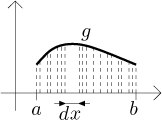
Jak už jsme viděli předtím, můžeme si představit, že se tato oblast skládá z nekonečně mnoha tenkých svislých proužků o šířce dx. Pokud tyto proužky začneme posunovat nahoru a dolů, výsledný obsah se nezmění. Toto je obecný princip, libovolná oblast může být rozložena na proužky a těmi pak hýbáno - musí ale být všechny rovnoběžné a musíme se všemi hýbat ve stejném směru - aniž by se změnil obsah. Například všechny obrazce na následujícím obrázku mají stejný obsah:

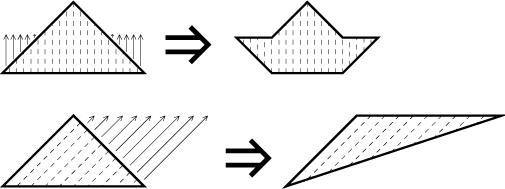
Dá se dokonce představit, že se dané těleso skládá z nekonečně mnoha paralelních tenkých válců a pak s nimi hýbat nahoru a dolů, tohle se používá při odvozování všelijakých vzorců.

Když jsme toto přijali, tak se teď podíváme na oblast pod grafem g, rozložíme ji na svislé pruhy a pak s nimi pohneme nahoru a dolů tak, aby nový spodní okraj měl přesně stejný tvar jako graf funkce f:

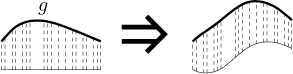
Pak tuto oblast zvedneme a položíme ji nahoru na graf f. Součtový vzorec by teď měla být jasný.

Nejen to, pokud jsme se spřátelili s pojmem dx, můžeme příslušný vzorec také dostat algebraicky. Zvolme nějaké x a uvažujme odpovídající svislý pruh v tomto bodě, se šířkou dx a sahající až po graf f + g. Výška ve středu tohoto sloupce je přesně f (x)+g(x), jeho obsah je tedy [f (x) + g(x)] krát dx. Sečtením obdržíme

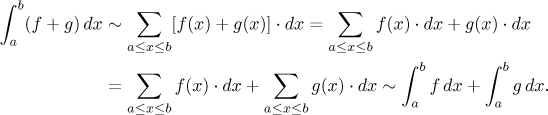
Samozřejmě jsme hodně podváděli, ale takhle to vypadá dost lehké k pochopení.