
In this section we will introduce the Newton integral. The idea is quite simple: the derivative tells us how to change functions into different ones. The Newton integral attempts to undo this procedure, to a given function we will try to find its antiderivative.
Definition.
Let f be a function defined on an interval I. We say that a function F on I is an antiderivative of f if F is continuous on I andF ′(x) = f (x) for all x from the interiorInt(I ) of I.
If such an antiderivative on I exists, then we say that f is (Newton-)integrable on I.
The definition is done in this way because we use the notion of
antiderivative in two settings. In order to have a derivative at a certain
point x, a function must be defined on a neighborhood of this point.
So the most natural situation is when we look for an antiderivative of
f on an open interval
However, often we need an antiderivative F on a closed interval
Example: The function
Indeed, F is continuous on the real line, so it is also continuous on
In the same way we check that also
This example shows several interesting things. First of all, how did we get these antiderivatives? We guessed using our experience with derivatives. Unlike the procedure of differentiation, where we had a reliable algorithm and could differentiate any function that comes our way, the antiderivative is a different story. We will get to it later.
The second interesting thing is that we can have more antiderivatives to the
same given function. Again, based on our experience, this should not be
surprising; for any constant C, the function
Are there also any other kinds of antiderivatives of
Theorem.
Let F be an antiderivative of f on some interval I.
(i) For any constant C, the functionG(x) = F(x) + C is an antiderivative of f on I.
(ii) If H is another antiderivative of f on I, then there is a constant C such thatH(x) = F(x) + C for all x from I.
The first statement is easy, since G is continuous where F was and
We can also consider this situation from a geometric standpoint. The
antiderivative condition
In the converse (ii) we are given a function f prescribing slopes of tangent lines of graphs of two functions, F and H. Imagine that we try to draw these two graphs. We start at their left endpoints and begin drawing both of them simultaneously. Since the two graphs have the same tangent lines at corresponding points, it means that they rise and fall in the same way; that is, we have to move the pencils in a parallel way.

Thus the graphs have to have the same shape, just shifted up or down.
There is no notation to express directly the fact that some F is an
antiderivative of f. However, there is a notation for the set of all
antiderivatives on a given interval. We denote it by
![]() .
This is called the Newton integral of f on I.
.
This is called the Newton integral of f on I.
Since the above theorem tells us exactly how the set of all antiderivatives looks like, we usually describe this set - the Newton integral - in the following way: If F is some antiderivative of f on an interval I, we write the set of all antiderivatives of f on I as
![]()
The process of finding an antiderivative is called integration.
Note that the notation is actually wrong. Since the antiderivatives form a set, the proper notation should be
![]()
However, this seems like too much writing, therefore people prefer the incorrect but easier notation. As long as we remember that the answer on the right hand side is a set (or, to put it another way, any function of the given form, where for C we can put an arbitrary constant), we should be fine. One frequent mistake is that people forget to put the "+C" there. This is a serious error, which in simple problems may look formal and like a nitpicking, but in applied problems this can be quite serious.
Example: The first example above can be written like this:
![]()
Unless the interval is somehow determined by the problem, we always try to put the largest interval possible. This is called the domain of the integral. We determine it by intersecting the domain of the integrated function with the domain of the antiderivative we find, perhaps removing some points where the antiderivative is defined but has some problem with its derivative. In the above example, the domain would be the whole set of real numbers.
Since the domain is the largest interval on which we can integrate, we can use the given answer also on "subintervals". It is clear from the definition that if F is an antiderivative of f on some interval I and J is an interval that is a subset of I, then F is an antiderivative of f on J.
The fact that there are many antiderivatives also has another consequence
that one has to keep in mind. Although we call the resulting function
antiderivative, the procedure does not undo the
differentiation process. Indeed, we know that the derivative of
If we use the Newton integral notation, this question of reversing does not even make sense. The outcome of the integral procedure is not one function but a set of functions, so it cannot be equal to the one given function that we started with and differentiated.
On the other hand, if we start with a function f, find an antiderivative F and then differentiate it, we end up with f again. This follows directly from the definition of an antiderivative. With the Newton integral notation this becomes a bit unclear: How do you differentiate a set of functions? But if we adopt a convention for a moment that this means differentiating all functions from the given set and making it into a new set, we can write (not precisely, but it captures the spirit):
![]()
Recall that when we introduced the integral notation, we started like this: "If F is some antiderivative of f on I..." How do we get this F? In fact, as we will see later, some functions do not have an antiderivative, in other words, the integration procedure fails! But before we get to it, we look at some properties of an antiderivative:
Theorem (linearity of integral).
(i) Let F be an antiderivative of f on some interval I. If k is a real number, then(kF ) is an antiderivative of(k f ) on I.
(ii) Let F be an antiderivative of f on some interval I, let G be an antiderivative of g on I. Then(F + G ) is an antiderivative of(f + g ) on I.
This theorem is actually very easy to prove. For instance, the function
(kF ) is continuous where F was and the differentiation
rules immediately yield
We can also express this theorem using the integral notation:
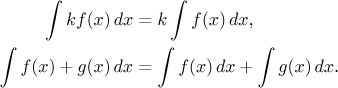
This notation is easier to use than the language of antiderivatives when it comes to actual integration. For instance, using our experience with derivatives we guess and easily write that
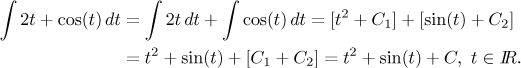
In the problem we used a different variable. Just like in the urit? integral, the variable is not really important here, what matters is the formulas. We just have to be careful not to change it by a mistake during calculations. A good habit is to check at the end that our answer has the same variable as the question. Note also that a sum of two constants whose values are arbitrary numbers is just one number, again arbitrary. When people integrate using the rules from the linearity theorem, they usually do not bother with putting more constants and write just one "+C" right away.
Another good habit is to check that we got the right answer. This is one and perhaps the only nice thing about integration. We can easily check that we got the right answer by differentiating it and comparing with the given function:
![]()
In the same way we check that the following list of elementary integrals based on derivatives that we remember is correct:
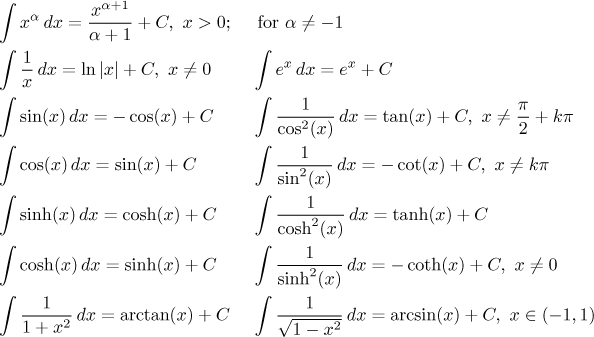
We only specified domains when they were different from the whole real line. Note that in some cases we did not put the domain of the integral properly. The reason is that we only define antiderivatives on intervals, that is, we are not allowed to put more complicated sets as domains. However, in some cases we have a choice between several possible intervals.
Therefore we introduce an important convention. When we put some conditions
instead of an interval as the integral domain, we can use this integral on
any interval that satisfies these conditions. In the first integral we
actually did not have a reason to avoid the proper notation, but writing
The second integral is a good example of our convention. We can use the
antiderivative
It is more complicated with the integral leading to tangent. The result is
true on any interval not containing the specified points. The largest
possible intervals are of the form
![]() .
.
The list can be surely made longer. Every derivative result that you remember can be put into this table in an integral form. However, the integrals above are the most important, you cannot hope to integrate successfully without knowing them by heart and at the same time, they should be enough for most problems. Of course, if you remember more, you chances of success increase.
This may be a good place to remark that when we integrate a fraction, people would often put the dx (or whatever differential we have) into the numerator to make it shorter. For instance, we write
![]()
We now look at a few problems where we also show some simple and popular tricks. We will write the first solution in detail, an experienced integrator would skip some steps.
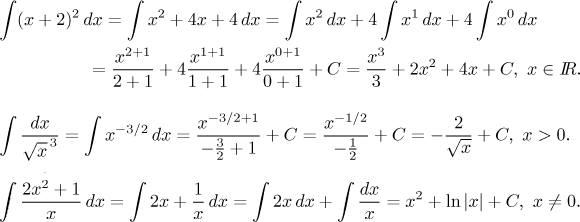
Check by differentiation that the answers are correct.
The procedure for integration that we just saw resembled differentiation in the way it works. You remember some elementary integrals, you remember some rules and the rest is algebra. Unfortunately, this is one of the disadvantages of integration, perhaps the main disadvantage. This impression about algebraic approach is quite correct; but unlike the case of differentiation, the linearity theorem shows the only two rules available for integration. There is no product rule, no quotient rule, no chain rule for composition of functions! Since most functions are somehow composed using products, ratios and compositions, this means that we would not know how to integrate them directly.
There are some specific rules that can help with special types of integrals. This is not such a good news as it sounds, because it means that the whole procedure becomes quite messy. Given an integral, one has to guess which procedure to apply, often some tricks are involved, sometimes simple, sometimes very difficult. Even a very simple function can take several pages to integrate. There are no algorithms that would tell you what to do next, the only guide is experience. If you want to become a successful integrator, a lot of practice is essential. We focus on this problem in the sections on Methods of Integration. In Theory - Integration methods we cover the specific rules and methods, in Methods Survey - Integration we try a practical approach.
We close this section with a brief look at the question of integrability.
Since the process of integration is rather difficult, it is probably not
surprising that for some functions it is impossible. This is the case of the
step function that we had as an
example in the section on Riemann
integral.
Here we will prove that this
function has no antiderivative on the interval
One good news is this:
Theorem.
If f is a continuous function on a closed interval I, then it has an antiderivative there.
Unfortunately, this theorem is not as good as it sounds. First of all, this theorem just says that the antiderivative exists, but not how to find it (quite typical in math actually). What is worse, the antiderivative that is guaranteed by this theorem can well be a theoretical function, which exists and one can draw its graph, but the graph is so strange that its shape cannot be expressed using any algebraic combination of elementary functions.
Such is the case of the function
![]()
This is a very nice function given by a simple expression, it is continuous on the whole real line. In fact, it is the famous "bell-shape curve" that is used in probability a lot (Gaussian curve):
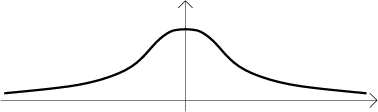
By the above theorem it has an antiderivative, this picture shows one of them:
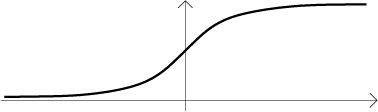
However, this shape cannot be expressed using elementary functions. No matter
what kind of an expression you write for F, you will never get
There are more functions of this kind, we list some of the nicer ones. The following integrals exist, but we cannot write the antiderivatives using elementary functions:
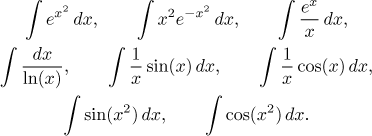
Remembering these can be useful, too - you know when to give up. At least for now. There is a way to express their antiderivatives using power series, but that belongs to another section entirely, see Applications of series in Series - Theory - Series of functions or this problem in Integrals - Solved problems - Integrals.
The Fundamental Theorem of Calculus
Back to Theory - Introduction