Example: Consider the function
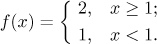
This function looks like this:
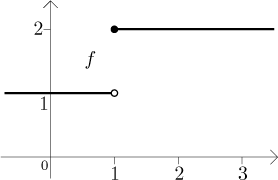
We claim that it has no antiderivative on [0,2]. We will prove
it by contradiction.
Assume that some function F is an antiderivative of f on
[0,2].
Then for x > 1 we have
F ′(x) = f (x) = 2,
while for x < 1 we have
F ′(x) = f (x) = 1.
What can be said about the derivative at
x = 1? Since F is an antiderivative, we
must have
F ′(1) = f (1) = 2.
Therefore also the derivative of F at 1 from the left must exist and
be equal to 2. However, since F is continuous at 1 from the left and
F ′ is continuous on (0,1) (a left
neighborhood of 1), we can use theorem
(see Derivative and limit in Derivatives - Theory - MVT) to
evaluate the left derivative at 1:
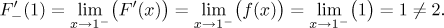
This contradiction shows that our assumption was wrong, F cannot be an
antiderivative of f.
![]()

![]()