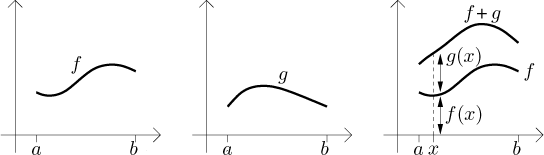
Consider two functions f and g defined on a closed interval [a,b]. Since the definite integral is related to area, and we will not present a proof, just an intuitive justification, we can afford to assume that both functions are positive. First we need to make sure that we understand how a graph of f + g is created. At each point x, we first go up by f (x), and then we go up once more, this time by g(x):

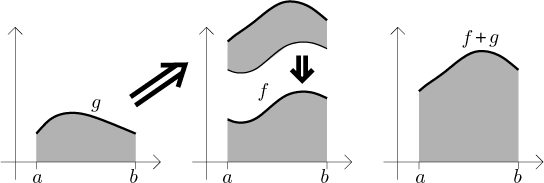
Now we should relate this resulting region to regions under the graphs of f and g themselves. Look at the graph of g:

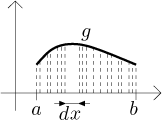
As we saw before, we can imagine that this region consists of infinitely many thin vertical strips of thickness dx. If we start moving these strips up and down, the resulting area should not change. This is a general principle, we can decompose any region into thin strips and manipulate them - as long as they are all in the same direction and we also move them in this direction - without changing the area. For instance, all figures in the following picture have the same area:

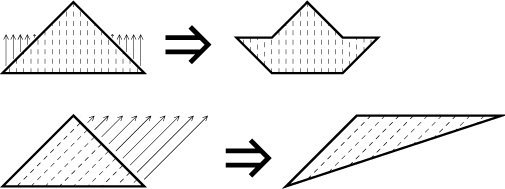
In fact, one can also imagine that a given solid consists of infinitely many thin parallel tubes and move them up and down without changing volume, this is often used when deriving all kinds of formulas.

Having accepted this, we now look at the region under the graph of g, decompose it into vertical strips and move them up in such a way that the new bottom contour of the region has exactly the shape of the graph of f:

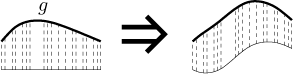
Then we move this region up and put it down on the top of the graph of f. Now the addition formula seems clear.

In fact, having accepted the dx idea, we can even get this algebraically. Pick some x and consider the corresponding vertical strip at that point, dx wide and going up to the graph of f + g. The height in the middle of this strip is exactly f (x)+g(x), therefore the area is [f (x) + g(x)] times dx. Summing up we obtain

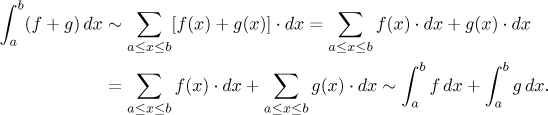
Of course we were cheating a lot, but it seems easier to understand this way.