Here we will use a physics setting to see why the fundamental theorems of
calculus could be true.
Let f (t) be a function defined on
[a,b]. We will
use the following interpretation:
Imagine that you are driving along a highway and at time
t = a, you pass a milepost that says
"000". You drive on and record the instantaneous speed on your
speedometer as f (t), until time
t = b. What is your position
F(x) at time
t = x along the highway, as measured by
mileposts? For details on this setup, see
this note
in Introduction to functions, but note that to illustrate the Fundamental
theorem properly we had to relabel functions. The position that we call
F here is called r in that note.
When you drive for t hours at a constant speed v, you cover
d = vt miles. However, this cannot be
used in our case, since the velocity changes all the time. Since this is a
real-life situation, we may assume that f is a "nice"
function. This means that if, at some time t, you look at it over
some really tiny time interval dt, the velocity almost does not
change. Therefore, the change of your position ds during the time
segment dt is f (t) times dt. The
total change in position (displacement) is obtained by summing all the tiny
changes over all possible time segments dt between
t = a and
t = x:
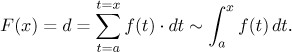
Now we also see why we cannot use x as a variable in the integral when
we use it as a limit of this integral. When we fix one such x, we
still want to be able to move along time as we add up the small velocity
contributions, therefore we need another variable.
In any case, we just saw that the position F(x)
is given by the above integral. Since we know from physics that the
derivative of displacement gives instantaneous velocity, we get
F ′ = f and F is an
antiderivative of f, exactly as claimed by TFC 1.
Now imagine that at time t = a, the
milepost does not say "000" but some other number. We will again use
F to record our position along the highway based on mileposts, in
particular, F(a) shows our position at the
beginning. From physics we know that F is an antiderivative of the
velocity f. The displacement (distance we drove) between times
t = a and
t = b can be calculated using the
position function F, but also summing up the velocities as above, and
we get
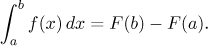
This is exactly the Newton-Leibniz formula.
This equality is sometimes stated in this way:
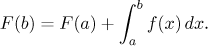
In our interpretation it means the following: To find your position at time
b, you start with the position at time a and add all the
displacements corresponding to your instantaneous velocity between times
a and b.
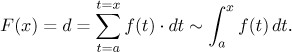
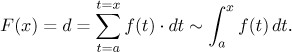
![]()
![]()