This box deals with integrals of "reasonable functions" that have instead of their variable a root of a certain expression, typically of x. Here is an example:
![]()
The method is quite simple. We use the substitution
![]() ,
where k was chosen so that in the resulting integral there are no
roots. There are many such k, but if we want the least possible (which
should simplify the calculations that would follow), we choose the least
common multiple of all roots appearing in the integral. In the above example
we would choose six (the least common multiple of 2 and 3) and obtain
,
where k was chosen so that in the resulting integral there are no
roots. There are many such k, but if we want the least possible (which
should simplify the calculations that would follow), we choose the least
common multiple of all roots appearing in the integral. In the above example
we would choose six (the least common multiple of 2 and 3) and obtain
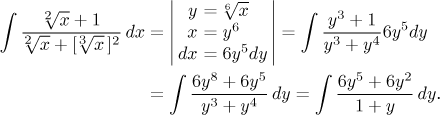
Note that in order to simplify calculations, we first solved the basic substitution equality for x and then used it to determine dx. It thus actually became an indirect substitution. This is exactly the recommended way of looking at this situation, since it can easily generalize to more interesting situations. Before we do so, for the sake of completeness we conclude this example. It is a standard problem, an integral of a rational function. The first step is to divide the numerator by the denominator, and it turns out that there is actually no remainder, so the problem is in fact very simple.
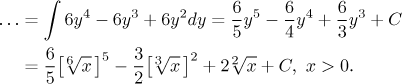
A more general situation occurs when in the root we find not just x,
but some other expression
Recommended procedure: We use the mixed substitution
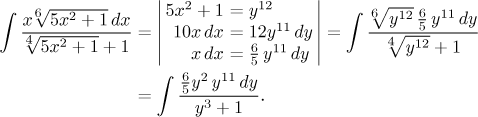
As usual we know that some substitutions will surely work, for instance when there is a linear expression under the root.
Other integrals of this type can be found in Solved Problems - Integrals. This one is really typical, the power-substitution trick is also used here and here.
Next box: integrals with ratios of linear functions
Back to Methods Survey
- Methods of integration