Here we focus on integrals of functions in which ainplace of x appears the fraction
![]()
We assume that this fraction cannot be simplified, algebraically this means that ad ≠ bc.
This type of integral can be handled using the substitution
![]()
Among the most popular examples of this type are rational functions featuring such fractions, often with the fractions under roots. We then combine tricks from this box and the previous box "integrals with roots".
Example:
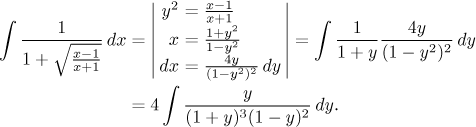
Next we apply the partial fractions decomposition. Two of the five constants can be determined by the "cover-up" trick, to get the remaining three we need three linear equations. Eventually we get partial fractions based on linear factors which we easily integrate. The result will be valid on intervals where the expression under the root is not negative.
Other examples of this type can be found in Solved Problems - Integrals, namely this and this.
Next box: trigonometric integrals
Back to Methods Survey
- Methods of integration