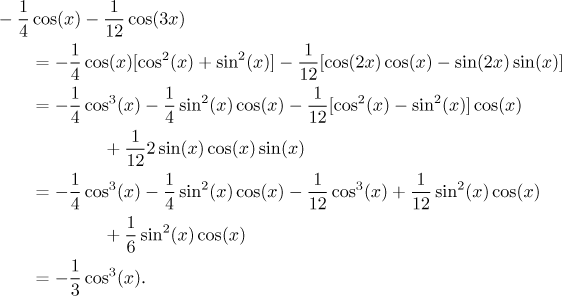Problem: Evaluate the integral

Solution: This looks like a simple integral. It fits the box "trigonometric integrals" and we see right away that there is an extra sine. This means that the cosine substitution will work; it will change this integral into an elementary one:

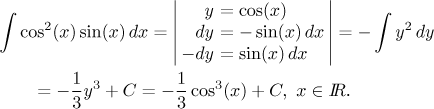
To get some practice, we try it another way. The expression in the integral is of the form sin^m(x)cosⁿ(x), for which we had a procedure in that box. It recommended to use identities to lower the power in exchange for a multiple at the variable.

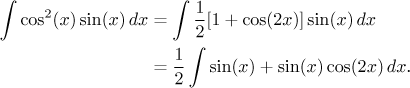
The next step is to use identities and rewrite the product as a sum. The rest is easy using linear substitution.

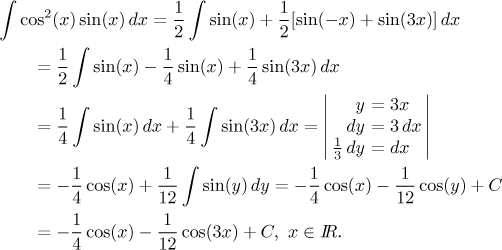
Is it the same answer as before? Yes.

Next problem
Back to Solved Problems - Integrals