Problem: Evaluate the integral
![]()
Solution: We never saw any formula for integrating absolute value, what should we do? As usual, when we see an absolute value, we try to get rid of it using a split definition:
![]()
Note that we somewhat unusually used equality in both versions, although the
reader is probably used to use first a non-sharp inequality and then a sharp
inequality in specification of validity. But it is not wrong here, since
when we take
So much for advance warning, we can integrate now.
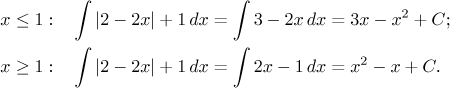
We obtained
![]()
However, this notation is definitely not the best one, since it suggests something that is just not true. It is definitely not true, that an antiderivative to the given one would be given as a split function by the formula on the right, the situation is in fact exactly as outlined above, on one interval we have one antiderivative and on the second interval a different one, also those C can have a different value for each version. The second last expression, with separate statement for each interval, is definitely better.
From practical point of view, if we want to integrate over an interval that fits the first condition, then we use the first formula. For intervals satisfying the second condition we use the second formula. So far so good. But what do we do when the interval we are given actually spans both regions, as we have in the given problem?
We already know that it would be a mistake to simply substitute 0 into the first formula and 4 into the second; just try it and you will see that you get something different from the correct answer below. There are two possible solutions, both based on The Fundamental Theorem of Calculus II that demands an antiderivative on the whole interval of integration.
One possibility is to split the integral into two parts.
![]()
Now we consider two functions:
![]()
The function G is everywhere continuous and differentiable, what we
really care about is that it is continuous on
![]()
This is usually the preferred way. A practical rule is simple, we simple use appropriate formulas on intervals, and if we do not have one, then we split intervals. We went through all those details to recall how all this is supported by theory.
An interesting alternative is to try to create an antiderivative to
First we check whether the two functions G and H happen to be connected at the point 1. The one-sided limits are simple.
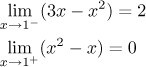
So we see that there is a jump at 1, the situation actually looks like this:
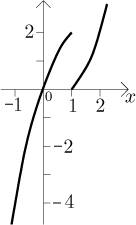
Therefore our first step is to create a continuous function on the real line by "gluing" the two branches together at 1. Since we do not want to spoil derivatives at other points, we do it by shifting the whole right branch up in such a way that it becomes connected to the left half. In this way slopes of its tangent lines (derivatives) stay the same.
![]()
The function F is continuous on the real line and since we kept the
original antiderivatives just shifted by a constant, we surely still have
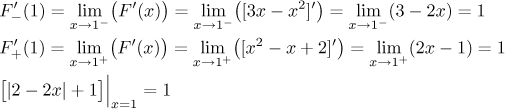
So the function F is indeed an antiderivative on the whole real line and we can substitute the limits into it:
![]()
We obtained the same answer, which is to be expected.