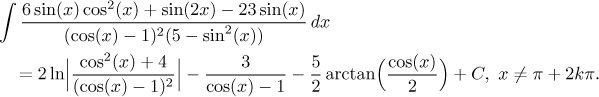Problem: Evaluate the integral
![]()
Solution: This integral fits into the box trig integrals, but not to any specific type there. It is really close to the last type, rational functions with sines and cosines, but for that we have a trouble with the doubling of argument in the sine on the top. However, this we can fix easily, then it looks like this.
![]()
Now it is an integral with sines and cosines only. We know that the universal substitution can rid us of trig functions, but we also know that it is an emergency solution that we prefer to avoid, here it goes like this. Usually we try to apply something easier, in the best case the sine or the cosine substitution. Will it work here? For the sine substitution we need to have a cosine next to dx, but it does not seem that we would be able to create it there is some reasonable way.
For the cosine substitution we need a sine next to dx and we can get it there easily by factoring it out of the numerator, so the cosine substitution will could work. Now we need to make sure that after we factor out that sine, only cosines will be left in the integral. Here the sine in the denominator starts troubling us, but fortunately it is squared there, so we can painlessly turn it into a cosine.
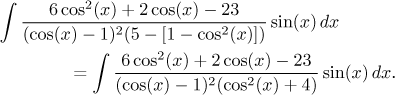
It worked, now we are ready for the substitution.
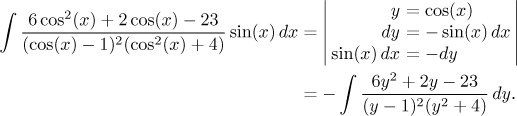
This is a classical integral of a rational function, so we proceed according to the appropriate algorithm. First we check that the degree in the numerator is smaller than the degree in the denominator, this is true. Then we should factor the denominator as much as possible, this is already done. Thus it is time to do partial fractions decomposition. There will be thre with four constants. One constant can be obtained easily by the cover-up method, the others out of three equations that we get for isntance using the multiplying mehod, but it will be a bit longer here. Therefore it might be an interesting alternative to try the limit method and the plug-in method. We show both approaches here, the reader will got he way he likes best. We get
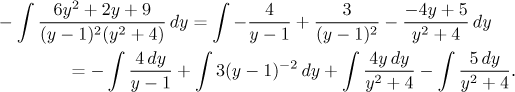
We split the quadratic fraction into two parts, since that's how we are supposed to integrate such a quadratic partial fraction, fortunately we did noy have to first complete a square in the denominator there. Now we will integrate. The first two integrals are elementary, the third is solved using a quadratic substitution. For the last one the standard algorithm recommends an indirect substitution.
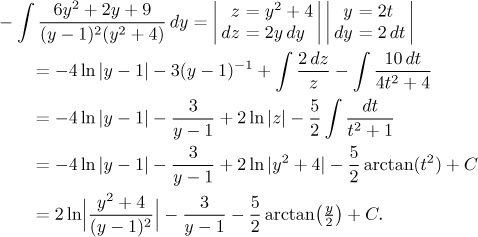
It remains to do the back substitution. What will the validity condition be? We see that y must not be 1, that is, cosine must be distinct from 1.