Příklad: Rozhodněte, zda tento integrál konverguje:
![]()
Řešení: Je tu jen jeden problém, v nekonečnu, a daná funkce je na integračním intervalu kladná, takže na daný integrál můžeme použít srovnávací testy. Zběžný pohled ukáže, že přímý výpočet je obtížný, ne-li nemožný, takže použití testů bylo moudré rozhodnutí. Všimneme si, že když x roste do nekonečna, můžeme ignorovat některé členy ve funkci (v obou polynomech přežijí jen nejvyšší mocniny):
![]()
Ověření:
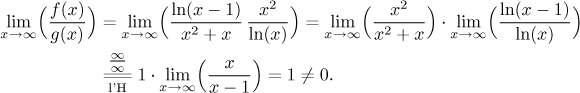
Dokonce máme i nerovnost, protože pro
![]()
S trochou štěstí by tedy mohlo pomoci i Srovnávací kritérium. Zbývá prozkoumání testovacího integrálu. Jednou z možností je přímý výpočet, nejprve je třeba najít primitivní funkci pomocí standardní integrace per partes:
![]()
Pokud neradi pracujete s logaritmy, je možné se jich zbavit substitucí, pak zase následuje integrace per partes:
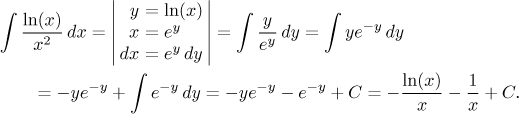
Proto
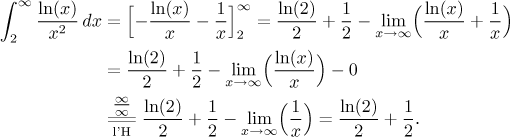
Testovací integrál konverguje, proto podle Srovnávacího kritéria (ale i Limitního srovnávacího kritéria) konverguje i daný integrál.
Poznámka: Existuje způsob, jak se vyhnout integraci testovací funkce.
Všimli jsme si, že logaritmy rostou pomaleji než libovolné mocniny. Protože
máme ve jmenovateli druhou mocninu, můžeme si dovolit kousek mocniny ztratit
a pořád ještě dostat konvergentní testovací integrál. Přesně řečeno, pomocí
argumentu s limitou se dá ukázat, že existuje jisté
![]() .
Pro
.
Pro
![]()
Dostali jsme novou a jednodušší testovací funkci. Protože víme, že integrál z h od K do nekonečna konverguje, podle Srovnávacího kritéria (a díky tomu, že mezi 2 a K není žádný problém) také konverguje daný integrál.