Integrování "per partes" je založeno na identitě, která se dá vyjádřit například vzorcem
![]()
(Viz integrace per partes v části Teorie - Metody integrace) pro jiné možnosti a další informace.) Hlavní myšlenka této metody je následující: Dostali jste integrál a povedlo se jej napasovat na integrál vlevo v oné identitě. Pak můžete přejít k výrazu napravo. To má samozřejmě smysl dělat jen tehdy, když je nový integrál napravo snažší (nebo stený, viz níže).
Algoritmus pro integraci per partes.
Krok 1. Vyjádřete si integrand jako součin dvou funkcí, jeden činitel
označte jako
Krok 2. Dopočítejte si ostatní výrazy z formule. Jmenovitě,
Krok 3. Dosadíte do per partesího vzorce. Výpočet per partes je hotov
a můžete se pokusit o vyřešení integrálu na pravé straně rovnosti.
Použití per partes se tradičně značí do matice, do prvního řádku se vepíše f a g', do druhého pak dopočítá f ′ a g. Ukážeme si příklad.
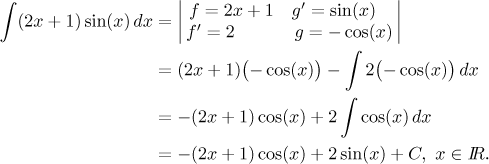
Poznamenejme, že celý výraz v daném integrálu musí být v postupu použit, takže když vynásobíme výrazy v prvním řádku matice, musí vyjít přesně výraz v integrálu. Není možné si kousek daného intgrálu nechat bokem. Jak vidíme, v druhém řádku matice pak najdeme nový integrál.
Zkušení integrátoři si tu matici někdy ani nepíší, integrace per partes funguje následovně: Nejprve jednu část daného výrazu zintegrujeme, dostaneme tak první nový člen, který už je hotov. V něm pak tu druhou část zderivujeme a dostaneme nový integrál.
Je třeba myslet na dvě věci. Za prvé, tu část, kterou hodláme integrovat
(neboli tu, kterou vybíráme jako
Za druhé, zbytek, tedy to, co budeme derivovat a označujeme f, by se
měl derivací výrazně vylepšit (právě zde by se mělo zabezpečit, že nový
integrál bude snažší). Když si zase představíme, jak vypadá výsledek
derivování různých výrazů, tak zjistíme, že i zde nemáme moc na výběr.
Když se to dá dohromady, skončíme v zásadě se třemi typy integrálů, na které má smysl integrování per partes aplikovat. Je dobré si je pamatovat.
• Typ "odstraňujeme x".
Integrál tohoto typu jsme už viděli v úvodním příkladě této sekce, v součinu
je funkce, kterou dokážeme snadno integrovat, vynásobená polynomem, který
pomocí derivování redukujeme. Základní příklady:
![]()
Volíme mocninu x (či obecněji polynom) jako f a onu pěkně
integrovatelnou funkci jako
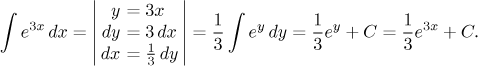
Teď už můžeme počítat následující integrál, jasný to kandidát na odstranění x pomocí per partes.
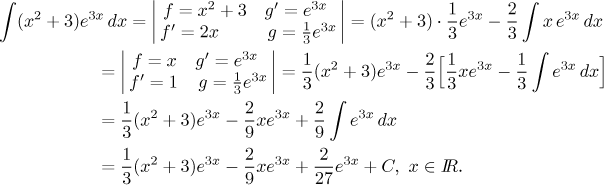
Typickou chybou při opakovaném per partes je zapomenout na tu závorku. Všimněte si, že bychom s touto metodou neuspěli, pokud by mocnina u x nebyla kladné celé číslo. Přesvědčte se sami, že například odmocniny z x se derivováním nezbavíte.
• Typ "odstraňujeme logaritmy".
Tento přístup je založen na tom, že derivací logaritmu získáme mocninu, takže
nový integrál již bude bez logaritmu. Postupu se tedy používá pro integrály
typu
![]()
Zde bereme naopak mocninu logaritmu jako f a mocninu x (či
polynom) jako
Velice zajímavý je ten poslední integrál. Asi jste si už dříve všimli, že
integrál logaritmu nápadně chybí v seznamu tabulkových integrálů. Logaritmus
totiž není derivací žádné elementární funkce a jeho integrál obvykle
vyhodnocujeme (pokud si jej nepamatujeme či někde nenajdeme) pomocí
integrace per-partes a zajímavé (a trikové) volby
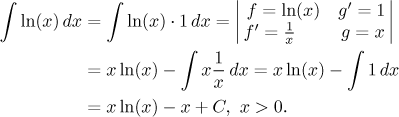
• Typ "odstraňujeme cyklometrické funkce".
Cyklometrické funkce jsou podobné logaritmu v tom, že když je zderivujeme,
tak dostaneme výraz úplně jiného typu, a to typu příjemnějšího z pohledu
derivace. Dá se tedy také aplikovat podobný trik na integrály jako tyto:
![]()
Jako příklad si ukážeme důležitý integrál arkus tangensu, kdy zase použijeme trik s jedničkou.
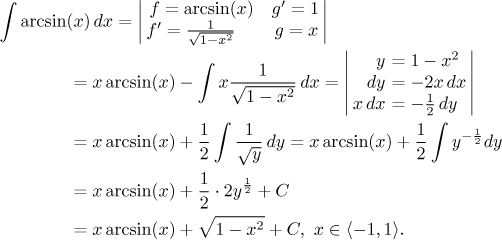
Čtenář se s integrací per partes asi setká nejčastěji právě u těch tří typů výše, metoda se dá ale použít i v jiných situacích, někdy docela překvapivě. Jeden docela užitečný trik si teď ukážeme.
Trik s rovnicí:
Tento trik se používá v případech, kdy po (několika krocích) per partes
skončíme s původním integrálem, ale s opačným znaménkem. To se nejlépe ukáže
na příkladě:
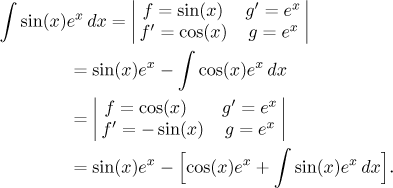
Dostáváme rovnici
![]()
Převedeme-li integrál z pravé strany na levou (přičemž je třeba mít na paměti, že jde o dvě množiny primitivních funkcí, které se mohou lišit o konstantu, proto na pravé straně tato neznámá konstanta zůstane), dostaneme
![]()
takže
![]()
(Zde jsme označili C=D/2. Jestliže je D nějaká (libovolná) konstanta, pak to platí i pro D/2, takže jsme oprávněni to označit jedním písmenem.)
Tento typ integrálu je docela užitečný v některých aplikacích a výsledek, který jsme právě odvodili, lze nalézt v rozsáhlejších seznamech integrálů. Dvě další situace s rovnicí se najdou v tomto příkladě a tomto příkladě v části Řešené příklady - Integrace.
Poznámka: Poznamenejme, že primitivní funkce, kterou si bereme jako g, nemusí být ta nejjednodušší, kdy za C volíme 0. Někdy je výhodné použít jinou hodnotu, aby nám pomohla s novým integrálem. Uvažujme následující příklad. Je to typický zástupce typu "odstraňujeme logaritmus" a my na něj použijeme integraci per partes obvyklým způsobem.
![]()
K dokončení příkladu bychom museli nejprve vydělit zlomek a pak integrovat zbytek, což není obtížné, ale proč pracovat, když nemusíme. Jednoduchý trik nás toho zlomku zbaví.
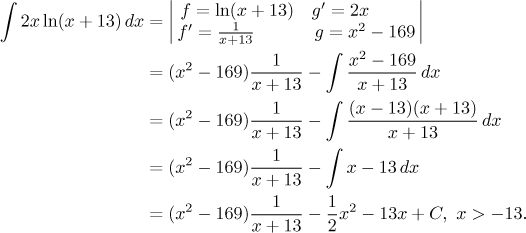
Mnohem lepší. Nestává se to natolik často, abychom o tom moc povídali, ale je dobré být si vědom toho, že máme při volbě g jistou svobodu.
Integrování per partes stojí také za některými užitečnými vzorci, viz tato poznámka a tato poznámka. Jak jsme také viděli, integrace per partes nám dává integrály několika základních funkcí, je to tedy metoda dosti důležitá. Typické použití lze nalézt v tomto příkladě, tomto příkladě a tomto příkladě v části Řešené příklady - Integrace.
Další šuplík: racionální lomená
funkce
Zpět na Přehled metod -
Metody integrace