Problem: Decide whether the following integral converges:
Solution:
There is just one problem, the infinity. So this is an improper integral of
the basic type with a positive function, and we can use convergence tests.
When x grows to infinity, in the numerator and the denominator the
highest powers prevail, after cancelling we can guess that our function looks
about the same as
If we want to prove this fact using the Comparison test, we would need to find an upper estimate. Unfortunately, this is not all that simple, since the desired inequality
is definitely not true (check). So instead we try the Limit Comparison test with our guess
This guess has to be justified:
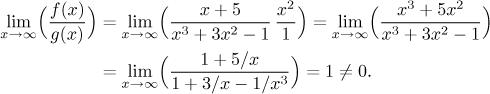
The limit condition is satisfied. Since we know that the test integral
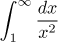converges, by the Limit Comparison test, the given integral also converges.