Problem: Decide whether the following integral converges:
![]()
Solution:
The integrated function is for
![]()
However, if we wanted to use this inequality with the Comparison test, it
would only work if the test integral was divergent. Then the given integral -
as a larger one - would also be infinite. However, when we look at the test
function, we should start having serious doubts. Note that exponential is for
large values of x much bigger than any given power. In particular, the
exponential in the denominator will definitely be larger than
![]()
However, the latter function has a convergent integral to infinity, so by comparison, also the function on the left should have a convergent integral. We will confirm this suspicion later. Just now it is enough to notice that we got a lower estimate for the given function, but unfortunately the corresponding test integral looks convergent, so it is one of those occasions when the Comparison test gives no conclusion. Instead we will use the Limit Comparison test.
When x grows to infinity, in the numerator x prevails, in the denominator the exponential prevails:
![]()
Now we have to justify our choice of the test function:
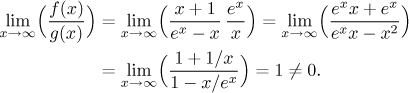
In the calculation we used the fact that near infinity, exponentials beat powers; to be precise,
![]()
The choice of the test function is justified. Now we need to decide on the convergence of the test integral. First we will find an antiderivative using integration by parts:
![]()
Thus the evaluation of the test integral leads to
![]()
The test integral converges, and therefore, by the Limit Comparison test, also the given integral converges.
Note:
We could have avoided the integration by parts by proving that there is some
![]()
Since we know that the integral of the function on the right from K to infinity converges, by the Comparison test, also the test integral for the Limit Comparison test converges, and therefore also the given integral converges.