Problem: Decide whether the following integral converges:

Solution: We know that there is no antiderivative for this function that we could write using elementary functions. Therefore we cannot evaluate this integral using standard methods. (By the way, one can find the value of this integral using a certain trick, it is half of the square root of π). We will try to use the Comparison test first, because it is easier (if it works) than the limit alternative.

What really bothers us in this integral is the square, without it it would be a simple integral. So we try to get rid of it. Clearly, for x ≥ 1 we have x ≤ x². Consequently also

Since the test integra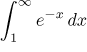l converges (see for instance here), by the Comparison test, also the smaller integral 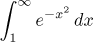converges.

On the interval [0,1] the given function is continuous, hence Riemann integrable. Putting it together with the result on the integral from 1 to infinity we see that the given integral is convergent.

Next problem
Back to Solved Problems - Improper Integrals