Problem: Decide whether the following integral converges:
![]()
Solution:
There is no obvious method for finding an antiderivative (check that
substitution and integration by parts do not help). Thus the only hope comes
from comparison tests. Since we have a natural bound for the sine function,
the absolute value version of the Comparison test seems like the natural
approach. Indeed, for all
![]()
We know that
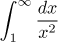 converges, so by the Comparison test, also the given integral converges.
converges, so by the Comparison test, also the given integral converges.
Notes:
1. In most problems on convergence testing, the Limit Comparison test is
something of a universal back-up approach. It helps when the simpler
Comparison test fails, and even if the Comparison test works, the limit
comparison can still be used. However, there are problems when this seemingly
reliable limit comparison fails - and this problem is one of them.
What happens when x grows to infinity? The square in the denominator
will behave - like a square, we cannot simplify it. In the numerator we have
an oscillating function, which we cannot ignore exactly because of this
oscillation. For instance, we may attempt to compare the given function with
![]()
does not exist. This shows that our comparison was wrong.
Similar calculation shows that also other powers cannot help. If we try to
increase the power from 2, the justification limit will still not exist. If
we try to use a lower power, the limit will be zero. Say, trying
![]()
(for instance by the Squeeze Theorem), so this comparison also failed.
This shows that powers do not help as test functions, similar argument rules out also exponentials. The conclusion is that the Limit Comparison test does not help here.
2. Consider the problem of convergence of
![]()
Again, this integral cannot be evaluated directly using the methods we know
now and the Limit Comparison test also fails as above. However, here we get
no help even from the Comparison test. Indeed, for
![]()
but we know that
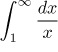 diverges and so no conclusion is possible.
diverges and so no conclusion is possible.
Since we did not cover any other test, this problem cannot be solved by the methods that we know right now. There is a tricky approach using series, see the appropriate exercise in Series - Exercises - Taylor expansion.