Délka křivky

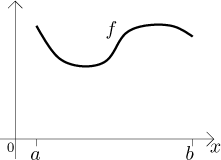
Uvažujme křivku danou grafem funkce f na intervalu ⟨a,b⟩.

Abychom našli její délku, rozdělíme interval ⟨a,b⟩ na části délky dx. Křivka se pak rozpadne na odpovídající části. Protože tyto kousky jsou velmi malé, můžeme předpokládat, že každý z nich je vlastně kouskem přímky.

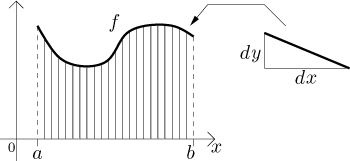
Délku takového kousku lze spočítat pomocí Pythagorovy věty. Na to potřebujeme znát délku vodorovné a svislé projekce. Horizontální velikost je dx. Protože zde máme přímku, odpovídající vertikální velikost najdeme vynásobením vodorovné velikosti dx směrnicí přímky, která je dána derivací f v x: dy = f ′(x)dx. Vlastně vzhledem k tomu, že y = f (x), by tato formulka pro transformaci diferenciálu neměla překvapit, už jsme ji viděli.

Sečtením délek všech kousků dostaneme délku křivky:

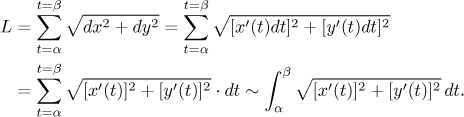
Teď už jen musíme zajistit, že dotyčný integrál existuje, například takto:

Fakt.
Uvažujme křivku danou grafem funkce f na intervalu ⟨a,b⟩. Jestliže má f spojitou derivaci na ⟨a,b⟩, pak délka této křivky je

Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩.

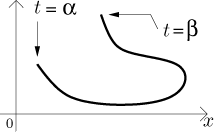
Zase máme dvě možnosti, jak délku křivky najít. Jedna je uvažovat funkci f generovanou pomocí y a inverzní funkcí k x, pak bychom použili substituce v již odvozeném vzorci pro délku.

Mnohem jednodušší bude přístup přes rozdělení křivky na malé kousky. Nicméně zde nebudeme dělit na kousky určené geometricky (například rozdělením osy x), ale rozdělíme časový interval ⟨α,β⟩ na kousky velikosti dt. Každý takový časový podinterval určuje kousek křivky. Přesně jako předtím budeme předpokládat, že díky své malé velikosti jsou tyto kousky přímé, a použijeme Pythagorovy věty k nalezení jejich délky. Substituční vzorec nám umožňuje určit dx a dy:

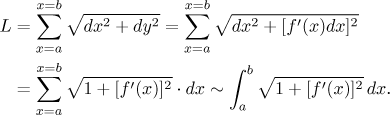
Abychom byli korektní, musíme zajistit, že integrál existuje a také že křivka necestuje po některé své části několikrát - pak by tato totiž byla započítána vícekrát.

Fakt.
Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩ takovou, že sama sebe protíná nejvýše konečně krát. Jestliže mají x a y spojité derivace na ⟨α,β⟩, pak je délka této křivky rovna

Uvažujme křivku danou v polárních souřadnicích předpisem ϱ = ϱ(φ) pro φ z ⟨α,β⟩.

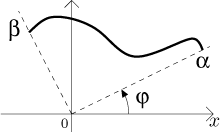
Zase jsou možné dva přístupy. Jeden je rozdělit úhel na malé podúhly velikosti dφ. Můžeme si představit, že odpovídající kousky křivky jsou přímé a najít jejich délku pomocí Pythagorovy věty:

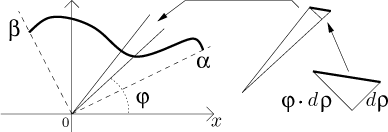
Všimněte si, že velikost "napříč úhlem" byla vypočítána podle vzorce "poloměr krát úhel" pro délku výseče kružnice, protože pro tak krátké kousky se délka části kružnice a délka odpovídající úsečky prakticky neliší. Kolmou část dϱ lze spočítat pomocí substituční formule z rovnosti ϱ = ϱ(φ). Sečtením dostaneme délku křivky:

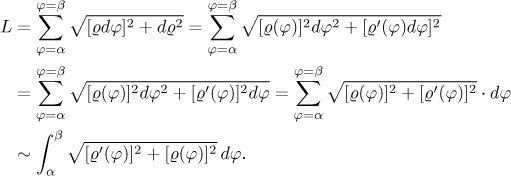
Je také možno přejít od polárních ke kartézským souřadnicím: x = ϱ(φ)cos(φ), y = ϱ(φ)sin(φ).

Tyto předpisy definují parametrickou křivku, takže můžeme použít příslušného vzorce:

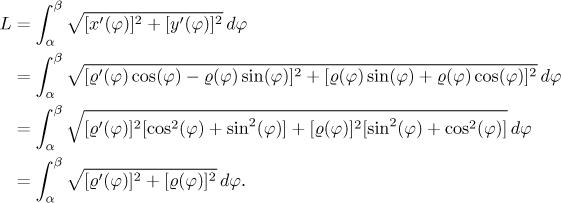
Abychom se vyhnuli problémům, měli bychom zajistit, že se žádná část křivky nezapočte několikrát. Zkusíme to nejjednodušším způsobem:

Fakt.
Uvažujme křivku danou v polárních souřadnicích předpisem ϱ = ϱ(φ) pro φ z ⟨α,β⟩, která sama sebe protne nejvýše konečně krát. Jestliže má ϱ(φ) spojitou derivaci na ⟨α,β⟩, pak je délka této křivky rovna

Objem rotačního tělesa
Zpět na Teorie - Aplikace