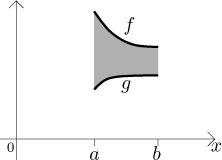
Uvažujme oblast R vymezenou shora grafem funkce f a zdola
grafem funkce g na intervalu

Nejprve předpokládejme, že funkce f je kladná a g je identicky nulová - tedy uvažujeme oblast pod grafem f. Zrotujme ji okolo osy x:
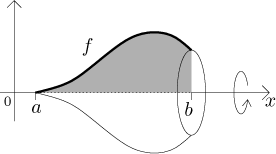
Abychom našli objem, rozdělíme osu x na kousky velikosti dx. Pro jeden takový kousek na pozici x je odpovídající svislý pruh pod grafem f tak tenký, že si jeho horní stranu můžeme představit jako přímku. Pokud pruh rotujeme, vzniklé těleso je vlastně komolý kužel.
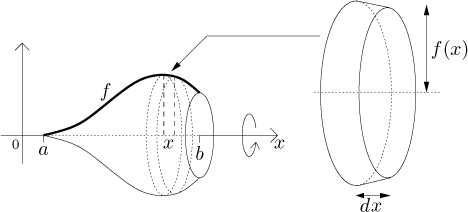
Protože je jeho výška dx tak malá, můžeme jej aproximovat válcem o
shodné výšce a s poloměrem rovným průměru horního a dolního poloměru kužele,
jmenovitě f (x). Objem takového válce je už lehký spočítat, je
to obsah základny krát výška. Protože mají tyto válce nekonečně malou výšku
dx, je vlastně lepší o nich přemýšlet jako o discích tloušťky
dx a poloměru
Sečtením objemů dostaneme
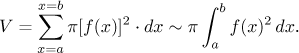
Teď se podíváme na oblast mezi dvěma grafy kladných funkcí, rotovanou okolo osy x:
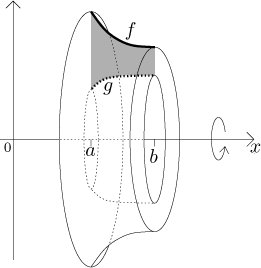
Objem tohoto tělesa je roven objemu celého tělesa určeného f mínus objem díry, což je těleso určené g:
![]()
Můžeme se na tento vzorec také dívat jako na součet objemů mnoha disků
určených rozdělením osy x na kousky o velikosti dx. Každý disk
má tloušťku dx, vnější poloměr
Pokud nakonec rotujeme okolo jiné vodorovné osy, dané rovnicí
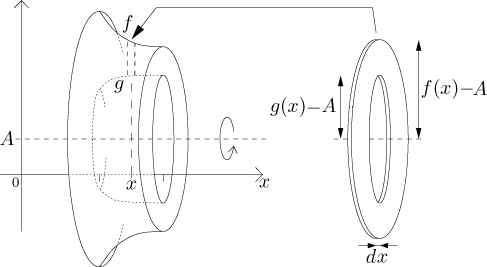
Dostáváme tedy následující:
Fakt (Metoda disků).
Uvažujme oblast R vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu⟨a,b⟩. Nechť A je číslo splňujícíA < min(g). Jestliže jsou f a g spojité, objem tělesa obdrženého rotací oblasti R okolo osy rotace dané rovnicíy = A je roven
Uvažujme oblast R vymezenou shora grafem funkce f a zdola
grafem funkce g na intervalu
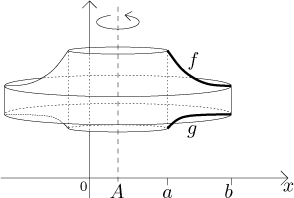
Protože teď už máme nějaké zkušenosti, zkusíme najít vzorec pro objem rovnou
pro tento obecný případ. Zase začneme rozdělením intervalu
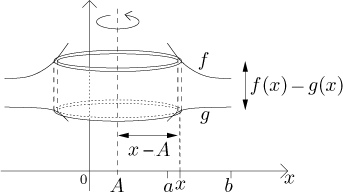
Protože je tak tenká, můžeme její objem aproximovat tím, že vynásobíme její
povrch tloušťkou dx. Jaký je povrch? Pokud slupku
"rozbalíme", dostaneme obdélník. Jeho výška je rovna výšce
rotovaného pruhu, což je
Můžeme tedy vypočítat objem jedné slupky. Celé těleso se teď dá rozložit na mnoho velmi tenkých slupek.
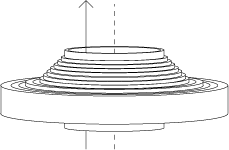
Sečtením jejich objemů dostaneme
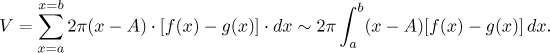
Jinými slovy máme následující:
Fakt (Metoda slupek).
Uvažujme oblast R vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu⟨a,b⟩. Nechť A je číslo splňujícíA < a. Jestliže jsou f a g spojité, objem tělesa obdrženého rotací oblasti R okolo osy rotace dané rovnicíx = A je roven
Uvažujme parametrickou křivku
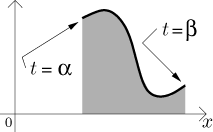
Teď budeme postupně rotovat tuto oblast kolem vodorovné a svislé osy a
najdeme výsledný objem. Bude to vlastně stejné jako předtím, protože
použijeme myšlenku z metody disků a metody slupek - vezmeme řez a rotujeme
jej. Jediný rozdíl je, že pro obě souřadnice máme parametrické vyjádření,
které se objeví jako poloměr disků, popřípadě jako výška a poloměr rotace
slupky. Změní se také tloušťka disku/slupky, kde použijeme transformační
vzorec pro diferenciál:
Fakt.
Uvažujme parametrickou křivkux = x(t), y = y(t) pro t z⟨α,β⟩. Předpokládejme, žey(t) ≥ 0 pro všechna t a žex(t) je monotónní. Předpokládejme rovněž, že y a x′ jsou spojité. Nechť R je oblast pod touto křivkou.Objem tělesa získaného rotací oblasti R okolo vodorovné osy rotace dané rovnicí
y = A, kdeA ≤ 0, je roven
Objem tělesa získaného rotací oblasti R okolo svislé osy rotace dané rovnicí
x = A, kdeA < min(x(t)), je roven