Hmotnost a těžiště

Úsečka

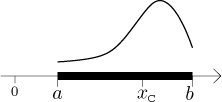
Její hmotnost je dána vzorcem

Její těžiště leží na ose x a jeho x-ová souřadnice je

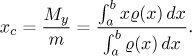
(Zde M_y je statický moment vzhledem k ose y.)

Křivka

Uvažujme graf funkce f na intervalu ⟨a,b⟩. Předpokládejme, že hustota v bodech této křivky je dána funkcí ϱ(x).

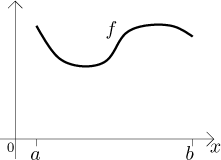
Hmotnost této křivky je dána vzorcem

Těžiště má souřadnice

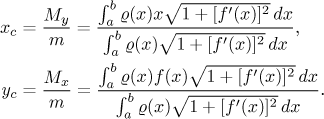
(Zde M jsou statické momenty vzhledem k příslušným osám.)

Rovinná oblast

Uvažujme rovinnou oblast vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu ⟨a,b⟩. Předpokládejme, že hustota v jednotlivých bodech oblasti závisí pouze na x a je dána funkcí ϱ(x).

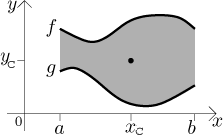
Hmotnost této oblasti je dána vzorcem

Těžiště je dáno

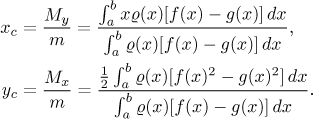
(Zde M jsou statické momenty vzhledem k příslušným osám.)

Rotační těleso

Uvažujme rovinnou oblast vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu ⟨a,b⟩. Předpokládejme, že hustota v jednotlivých bodech oblasti závisí pouze na x a je dána funkcí ϱ(x).

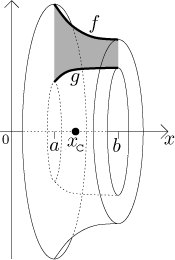
Pokud tuto oblast zrotujeme okolo osy x, výsledné těleso má hmotnost

Těžiště leží na ose x a jeho x-ová souřadnice je

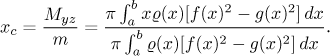
(Zde M_yz označuje statický moment vzhledem k rovině yz.)

Poznamenejme, že ve všech těchto situacích je nejobvyklejší případ, že je daný materiál homogenní, neboli hustota je vždy stejná. V tomto případě je funkce hustoty ϱ(x) vlastně konstanta, takže se ve vzorcích pro těžiště vždy vykrátí.

Parametrická křivka

Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Předpokládejme, že y(t) ≥ 0 pro všechna t a že x(t) je rostoucí:

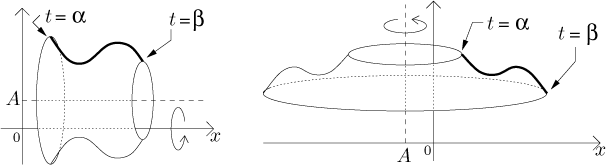
Pro zjednodušení budeme uvažovat homogenní útvary. Jejich hmotnost je pak dána jako délka/obsah/objem (viz příslušné sekce) násobený danou konstantní hustotou. Teď se podíváme na těžiště, v jehož vzorcích se hustota vykrátí.

Těžiště křivky samotné má souřadnice

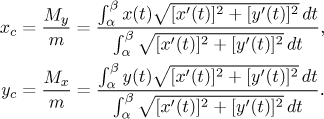
Těžiště oblasti pod touto křivkou má souřadnice

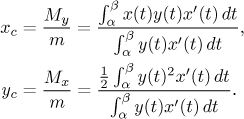
Těžiště povrchu získaného rotací této křivky kolem osy x leží na ose x a jeho x-ová souřadnice je

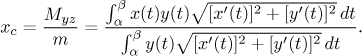
Těžiště tělesa získaného rotací oblasti pod křivkou kolem osy x leží na ose x a jeho x-ová souřadnice je

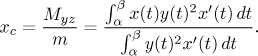
Všimněte si, že jsme v posledních dvou zlomcích zkrátili 2π v předposledním a π v posledním. To znamená, že pokud byste potřebovali samotné momenty, musíte vzorce z těchto čitatelů vynásobit odpovídajícím faktorem (a ve všech parametrických vzorcích také hustotou).

Derivace integrálu
Zpět na Přehled metod - Aplikace