Volume of a solid of revolution

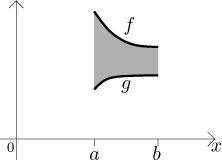
Consider the region R bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b].

Rotation about a horizontal axis

First assume that the function f is positive and g is identically zero - that is, we consider the region under the graph of f. We revolve this region about the x-axis:

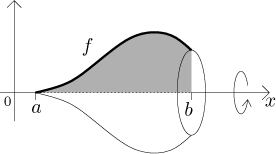
To find the volume, we split the x-axis into segments of size dx. For one such segment positioned at x, the vertical strip under the graph of f is so thin that we can think of its top as a straight line. If we rotate it, the resulting solid is actually a truncated cone.

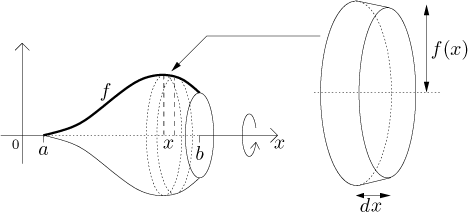
Since its height dx is so small, we can approximate its shape by a cylinder of identical height and with radius equal to the average of the top and bottom radius of the cone, namely f (x). The volume of such a cylinder is easy to calculate, it is the area of the base times the height. In fact, since these cylinders have infinitely small heights dx, it may be better to think of them as discs with thickness dx and radii f (x). If we do this procedure for each segment on the x-axis, we actually approximate the whole solid by suitable discs:

Summing up the volumes we get

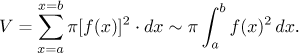
Now we look at a region between two graphs of positive function rotated about the x-axis:

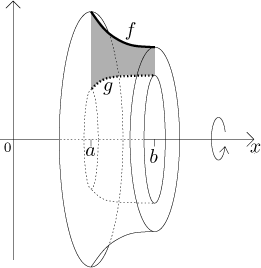
The volume of this solid is the volume of the whole solid determined by f minus the volume of the hole, which is the solid determined by g:

We can also see it as a sum of many discs with holes determined by splitting the x-axis into segments of size dx. Each disc has thickness dx, the outer radius is f (x) and the radius of the hole is g(x).

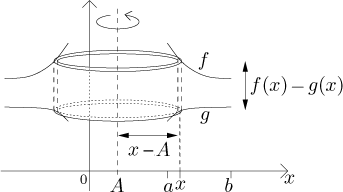
Now if we rotate about a different horizontal axis given by y = A, where A < min(g), it means that the radii of discs decrease exactly by A.

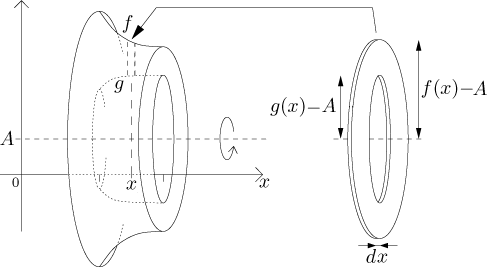
Thus we get the following:

Fact (Disc method).
Consider the region R bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b]. Let A be a number such that A < min(g). If f and g are continuous, the volume of the solid obtained by rotating the region R about an axis of rotation given by y = A is equal to

Consider the region R bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b]. Let A be a number such that A < a and imagine the solid obtained by by rotating the region R about a vertical axis of rotation given by x = A.

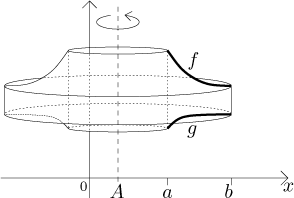
Since we now have some experience, we will try to deduce the volume formula directly for this general case. Again, we start by splitting the interval [a,b] into subintervals of size dx. Pick a subinterval at some position x. Consider the corresponding vertical strip between f (x) (top) and g(x) (bottom). Again, since the strip is so narrow, we may assume that the top and bottom are level (in other words, that the two functions are constant there). If we rotate this strip about the axis x = A, we get a very thin shell.

Since it is so thin, we can approximate its volume by multiplying its surface by its thickness dx. What is the surface? By unwrapping the shell we obtain a rectangle. Its height is equal to the height of the rotated strip, that is, f (x) − g(x). Its width is equal to the circumference of the shell, or, to the distance traveled by the revolving strip. This is equal to 2π times the radius, which is x − A.

So we can calculate the volume of one shell. The body can be decomposed into many very thin shells.

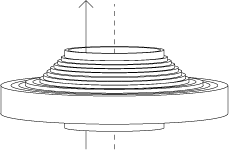
Adding all their volumes we get

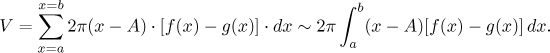
In other words, we have the following:

Fact (Shell method).
Consider the region R bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b]. Let A be a number such that A < a. If f and g are continuous, the volume of the solid obtained by rotating the region R about an axis of rotation given by x = A is equal to

Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and x(t) is increasing. Consider the region under this curve:

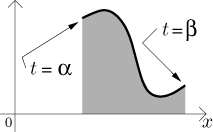
Now we will rotate this region in turn about a horizontal and vertical axis and find the resulting volume. The calculations will actually be just as above, since we again use the idea of the disc method and the shell method - take a slice and revolve it. The only difference is that now we have parametric expressions for the coordinates, which will appear as radii of discr, respective heights and radii of rotation of shells. Also the thickness of a disc/shell will be different, we use the transformation formula for differential: dx = x′(t)dt (see area). Thus we get

Fact.
Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and x(t) is monotone. Assume also that y and x′ are continuous. Let R be the region under this curve.

The volume of the solid obtained by revolving the region R about a horizontal axis of rotation given by y = A, where A ≤ 0, is

The volume of the solid obtained by revolving the region R about a vertical axis of rotation given by x = A, where A < min(x(t)), is

Surface of a solid of revolution
Back to Theory - Applications