Surface of a solid of revolution

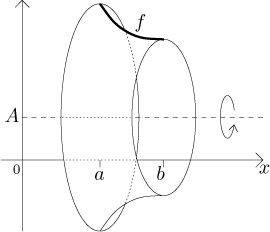
Consider the graph of a function f on an interval [a,b].

Horizontal axis of rotation

Consider the surface obtained by revolving this graph around an axis of rotation given by y = A, where A < min( f ).

To find the resulting surface area, we split the interval [a,b] into disjoint subintervals of size dx. For each such subinterval, consider the corresponding piece of the graph of f. Since the subinterval is very small, we may assume that the graph of f on this subinterval is a piece of the straight line whose slope is given by f ′(x). Therefore we can use the Pythagoras rule to calculate its length, just like we did it when calculating the curve length.

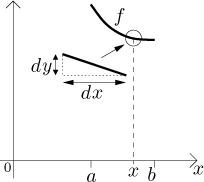
When we revolve this piece of graph, we get the outer surface of a truncated cone. To find its surface area, we multiply the size of this piece of graph by the distance traveled by its middle, that is, 2π times the radius, which is f (x) − A. This we do for all subintervals of [a,b], which means that we are approximating the surface of revolution by sides of truncated cones.

Adding up their surfaces areas we get

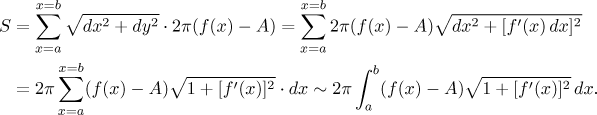
As usual, to ensure integrability we use the simplest way and require continuity:

Fact.
Consider the surface obtained by revolving the graph of a function f on an interval [a,b] around an axis of rotation given by y = A, where A < min( f ). If f has a continuous derivative on [a,b], then the surface area of the surface is equal to

Consider the surface obtained by revolving the graph of f about an axis of rotation given by x = A, where A < a.

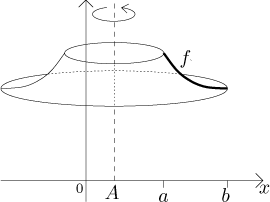
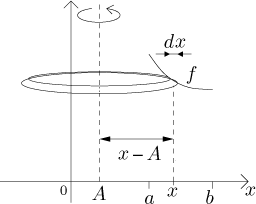
Here the procedure is almost identical to the above. We split the graph into little pieces corresponding to subintervals of size dx on the x-axis. Their lengths can be calculated just like above, then we revolve the pieces around. The only change is that now the radius of rotation is given by x − A for a piece of the graph corresponding to the subinterval at position x.

For the surface we therefore get

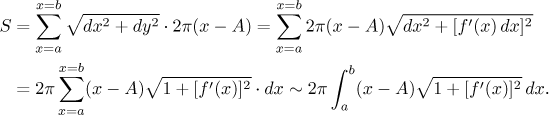
Thus we have the following:

Fact.
Consider the surface obtained by revolving the graph of a function f on an interval [a,b] around an axis of rotation given by x = A, where A < a. If f has a continuous derivative on [a,b], then the surface area of the surface is equal to

Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and x(t) is increasing:

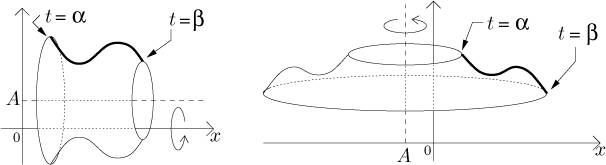
Now we will revolve this curve in turn about a horizontal and vertical axis and find the surface area. But this will now be easy. First we find the length of a small piece of the curve using the Pythagoras rule exactly as we did when calculating curve length. Then we revolve this piece and find the circumference just like in the previous calculation, we just have to substitute the parametric expressions. Thus we get:

Fact.
Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and x(t) is monotone, assume further that both functions have continuous first derivative.

The surface area of the surface obtained by revolving this curve about a horizontal axis of rotation given by y = A, where A < min(y(t)), is

The surface area of the surface obtained by revolving this curve about a vertical axis of rotation given by x = A, where A < min(x(t)), is

Mass and center of gravity
Back to Theory - Applications