Mass and center of gravity

Segment

Consider a segment [a,b] on the x-axis with density given by ϱ(x).

We split it into small pieces of size dx.

We may assume that on a piece at position x, due to its tiny size the density does not change and is equal to ϱ(x), therefore the mass of this little piece is ϱ(x) times dx. Summing up masses of all pieces we get the formula for the mass of the segment:

The center of mass lies on the x-axis. To find its x-coordinate we must first imagine that the segment is spinning around the y-axis and calculate its moment of rotation M_y. We know how to do it for point mass: M is the radius of rotation times the mass. Therefore if we split the segment into tiny subsegments of size dx, we can calculate in this way the moment of rotation for each piece: M = xϱ(x)dx. Summing them up we get the total moment:

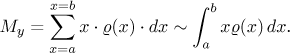
The x-coordinate of the center of mass satisfies the equality M_y = mx_c. This is simple to solve:

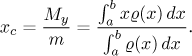
Consider the graph of a function F on an interval [a,b]. We assume that the density of mass at points of this curve is given by the function ϱ(x).

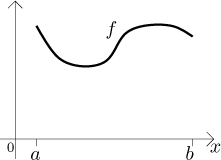
We split the interval [a,b] into small pieces of size dx. For such a piece at position x we consider the corresponding piece of the graph of f. Since it is so small, we may assume that it is a piece of a straight line and find its lenght as we did when determining curve length. Because thanks to this small size we can also assume that the density does not change and is equal to ϱ(x), so by multiplying density by length we get the mass of this particular piece. Then the total mass of the curve can be found by adding masses of all pieces via integration:

In order to find the coordinates of its center of mass, we have to find moments of rotation with respect to both axes. We split the graph as before and find the mass of a certain small piece corresponding to x. The moment of this particular piece with respect to the y-axis is calculated by multiplying its mass by the distance from the y-axis, which is x. The moment of this particular piece with respect to the x-axis is calculated by multiplying its mass by the distance from the x-axis, which is f (x).

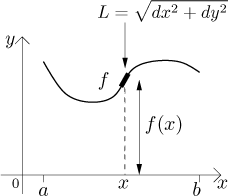
When we add these moments by integration, we get corresponding moments for the whole curve. Dividing by the mass we get the coordinates of the center of gravity, since they have to satisfy the same equations as we saw with segment above:

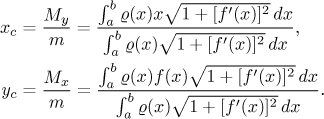
Consider a plane region bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b]. Assume that the density at points of this region depends only on x and is given by ϱ(x).

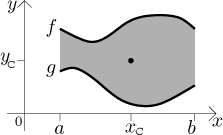
We split this region into vertical strips of width dx. On each such strip, the density can be assumed to be constant, so the mass is equal to the density times the area of the strip, which is the width dx multiplied by the height in the middle.

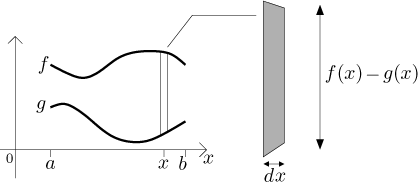
Summing up the masses of strips we get the formula for the mass of this region:

In order to find the coordinates of its center of mass, we again have to find moments of rotation with respect to both axes. First we determine the moment with respect to the y-axis.

Since on each strip we may assume a constant density ϱ(x) and each point of such a strip has equal distance from the axis of rotation, the moment of rotation of the whole strip is given by its mass ϱ(x)[f (x) − g(x)]dx multiplied by the moment of rotation of one point mass as above. Summing up the moments of all strips we get

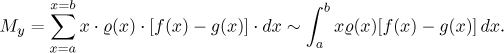
Now we will try to determine the moment of rotation with respect to the x-axis. This will not be so easy, because when we consider one strip as above, its points have different distance from the x-axis, the axis of rotation. Note that it would not make our work easier if we try decomposition into horizontal strips. The fact that points of one such strip have different density are bad enough, but the worst problem would be that we would have strips of different kinds. Some go from a to b, some just from a to the graph of f etc., in general this could be even worse.

So we are stuck with our vertical strips. We will handle the moment of rotation of one such strip as an independent problem. Note that in fact this is easy, we are revolving a segment [f (x),g(x)] about a horizontal axis, so if we flip the axes, we get the same picture as in the beginning:

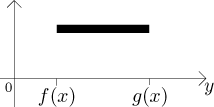
So we can find the moment of rotation just like we did with a segment, we just have to use the variable y and remember that the density is constant:

This was the moment for a segment, when we multiply it by dx, we get the moment of the strip. Summing up the moments of all strips we get the moment of the whole region with respect to the x-axis:

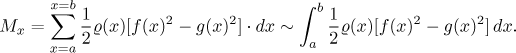
We find the coordinates of the center of gravity using the moments in the same way as we did it for the curve, so

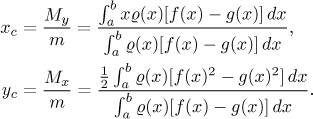
Consider the plane region bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b]. Assume that the density at points of this region depends only on x and is given by ϱ(x). This region is rotated about the x-axis, producing a solid:

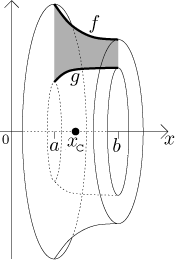
To find the mass, we consider vertical strips in the region of width dx. After revolving such a strip, we get a disc with a hole in the middle. Note that the density of points on such a disc can be considered constant, because it is so thin that the density should not change much (it depends on x only). Therefore the mass is the constant density times the volume of the disc, which we calculate just like when we were calculating the volume of solids of revolution using the disc method. Adding the discs up we get the total mass:

The center of mass lies on the x-axis. To get its x-coordinate, we need to find the moment with respect to the yz-plane. To this purpose we again use the above discs. Note that for one such given disc, all points of it have the same point mass (as they have the same density) and also the same distance from the yz-plane. Therefore its moment can be calculated by the distance x times the mass of the disc. Adding all moments up we get

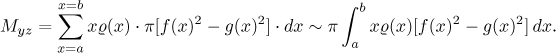
And just like before, the x-coordinate of the center of gravity satisfies M_yz = mx_c. Thus we get

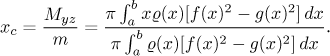
Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and x(t) is increasing:

For simplicity we will only consider homogeneous objects. Theor mass can then be calculated as their length/area/volume (see corresponding sections) multiplied by the given constant density. Now we will look at density, in the formulas the density will cancel out.

The calculations are actually the same as before, each object is decomposed into small pieces and moments are calculated. The only difference is that parametric equations enter into considerations, but we already developed necessary methods in sections on area and curve length. Thus we get the following:

Fact.
Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and x(t) is increasing. Assume also that both functions have continuous first derivative.

The center of gravity of the curve itself has coordinates

The center of gravity of the region under this curve has coordinates

The center of gravity of the surface obtained by revolving this curve about the x-axis lies on this axis and its x-coordinate is

The center of gravity of the solid obtained by revolving the region under this curve about the x-axis lies on this axis and its x-coordinate is

Note that in the last two fractions we cancelled 2π in the second last and π in the last. That is, if you need just the moments, the expressions in these numerators have to be multiplied by these two factors (and in all parametric formulas by the density).

Derivative of an integral
Back to Theory - Applications