Summing up series

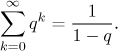
We will see that it is often relatively easy to determine that a given series is convergent. However, finding its sum, the number to which it converges, is a surprisingly difficult question. There is no general approach one could try; instead, the results that we know are often byproducts of rather involved calculations in different parts of mathematics. This is the reason why the problem of summing up a series is usually only touched upon in calculus courses. We will do pretty much the same here. First we introduce two cases when we do know how to get the sum, geometric and telescopic series. Then we introduce an approach via Taylor series that sometimes has a good chance to succeed. At the end we recall some formulas for sums of powers.

We already hinted in the previous paragraph that summing up series precisely, using calculations, is a tough business; thus it is to be expected that for many, perhaps most series the methods described below (and other methods) fail. What can we do then? We try to approximate, of course, which is the topic of the next section. Now back to our methods.

There is one series everybody can sum up - namely the geometric series. Here the situation is very simple, it is enough to remember the following formula.

Fact.
If |q| < 1, then

Considering that this is a formula for just one type of series, it is surprising how often it can help. Sometimes the given series is geometric in disguise and one has to work a bit to put it into the proper form.

Example:

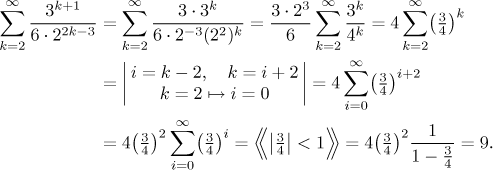
Instead of doing formally the substitution one can simply take and factor (3/4)² out of the geometric series. If you happen to remember the more general formula (geometric series sum for indexing starting at n₀), you can skip the substitution and apply the formula right there.

By a telescopic series we mean any series of the form  (b_k − b_k+1). The reason why it is called this way becomes obvious when we try to figure out its partial sums.

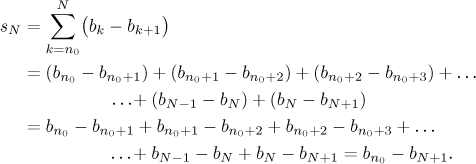
As we can see, the series folded on itself like a pirate's telescopic sight. Since convergence of a series is given by convergence of partial sums, we get the following statement.

Fact.
A telescopic series  (b_k − b_k+1)  converges if and only if the sequence {b_k} converges. Then also

The choice of order of terms in the definition of telescopic series was arbitrary, we could also define a telescopic series as the series of terms (b_k+1 − b_k). Then an analogous fact about its convergence and sum is true, just the formula for sum has the terms of the right hand-side switched as well (which is natural, if we switch at one end, we have to switch at the other one as well). In practice one usually does not remember the formula itself but rather the procedure, because it can help also with other types of series. The example just coming up shows that also a telescopic series can be disguised.

Example: Find the sum of

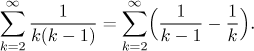
We have a telescopic series. To determine its convergence or divergence we check on its partial sums and then pass to a limit.

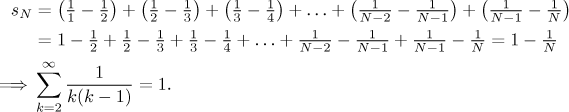
Telescopic series are rather rare, this notion is definitely way less useful than the geometric series above.

Sometimes we get a very useful information about the sum of a series if we artificially introduce a term x^k into it, which gives raise to a power series. We have to do it in such a way that when we substitute a certain constant for x, we get back the given series. One popular choice is to replace 1 with x^k, then after substituting 1 for x we get back our series. Some typical examples:

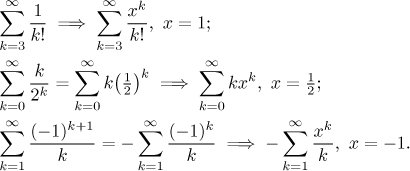
For instance, if in the second case we put x = 1/2, we get the original series. Why should it help if we make the problem more complicated? Sometimes we can figure out that the power series on the right is actually equal to some function f (x). Then we can try to substitute the right constant for x (see previous paragraph) both in the series and in f and with a bit of luck we find the sum of our series.

Example: We will try to find the sum of the alternating harmonic series 1 − 1/2 + 1/3 − 1/4 + ... The last example above shows the natural way of turning the alternating harmonic series into a power series. By a remarkable piece of luck, that power series is exactly the Taylor expansion of the function ln(1 − x) (see Taylor series in Theory - Series of functions). Therefore if we substitute x = −1 into this power series, we get the alternating harmonic series, but this should be the same as substituting x = −1 into ln(1 − x). Thus we get

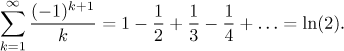
We know that for every positive q we have  ∑ k^q = ∞. Thus the case of infinite sum is trivial, but finite sums - partial sums of such series - appear quite often and it is nice to know that we have formulas for them for integers q. Probably the most famous is

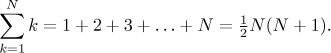
The proof is actually quite simple and uses the telescopic effect described above.

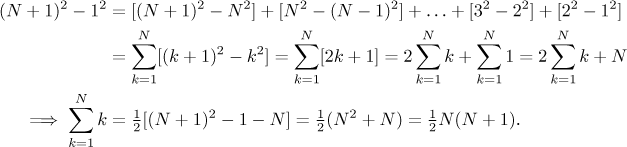
Higher powers have more complicated formulas and they are less popular, sometimes one can encounter sums of squares and cubes.

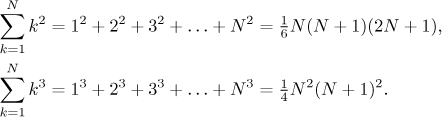
Proofs are similar and require knowledge of "lower" sums, for instance the sum of squares goes like this.

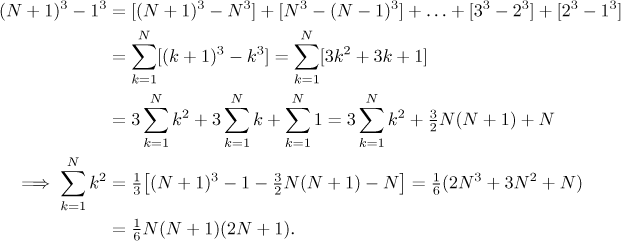
For more examples see Methods Survey - Summing up series and Solved Problems - Summing up series.

Approximating series, error of approximation
Back to Theory - Introduction to Series