Konvergence posloupností funkcí: Přehled metod

Je dána posloupnost funkcí { f_k(x)} a předpokládáme, že průnik všech jejich definičních oborů není prázdný. Obvykle se ptáme na dvě věci: Jaká je limita této posloupnosti a zda konverguje alespoň někde stejnoměrně.

Otázka 1: Vyšetřete (bodovou) konvergenci dané posloupnosti funkcí.
Řešení: Uvažujte obecné x z průniku definičních oborů, vemte to jako pevný parametr a vypočítejte limitu posloupnost reálných čísel { f_k(x)} pro k jdoucí do nekonečna.
Pro některá x to bude divergovat. Pro některá x tato limita konverguje, nazvěte výsledné číslo f (x). Množina všech x, pro které tato limita konverguje, tvoří obor konvergence, na něm dostáváte popsaným postupem funkci f a řekneme, že tam posloupnost { f_k} konverguje k f.

Otázka 2: Vyšetřete stejnoměrnou konvergenci dané posloupnosti funkcí.
Řešení: Nejprve najděte limitu f posloupnosti { f_k} dle předchozího návodu.
Dále odhadněte množinu M (podmnožinu oboru konvergence), na které by mohla být stejnoměrná konvergence. Typicky se začne s oborem konvergence, popřípadě oborem konvergence bez malých okolí jeho krajních bodů.
Pro pevné k vypočítejte

M_k = sup{| f (x) − f_k(x)|,  x z M }.

Jestliže M_k→0 pro k jdoucí do nekonečna, tak je stejnoměrná konvergence na M dokázána.
Jestliže ne, pak byla nejspíše množina M příliš odvážná. Zkuste si tipnout menší množinu, analýza onoho suprema by měla pomoci v určení, které části původní M dělaly problémy.

Příklad: Vyšetřete konvergenci posloupnosti

Řešení: Nejprve prozkoumáme konvergenci. Uvažujeme x jako parametr a spočítáme limitu vzhledem k k.

Tato limita existovala pro všechny hodnoty x, takže obor konvergence je celá reálná osa a daná posloupnost tam konverguje k funkci f (x) = x².

Je tato konvergence stejnoměrná? Podíváme se na rozdíl. Pro jedno určité k dostáváme

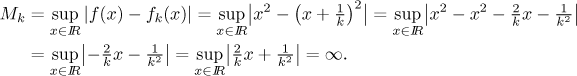
Protože jsou všechna suprema nekonečno, není možné, aby šla k nule, tudíž nemáme stejnoměrnou konvergenci na celé reálné ose. Problém je evidentně v tom, že x může být libovolně velké. Odhadneme tedy, že budeme mít lepší šanci, pokud budeme zkoumat stejnoměrnou konvergenci na uzavřeném intervalu M = ⟨-a,a⟩ pro libovolné kladné a. Teď dostáváme

Když pošleme k do nekonečna, tak jde M_k k nule, což dokazuje, že daná posloupnost { f_k(x)} konverguje k f (x) = x² stejnoměrně na každém intervalu typu M = ⟨-a,a⟩ pro kladné a.
Podobný argument by ukázal trochu obecnější fakt, který je i snažší zformulovat: Konvergence je stejnoměrná na libovolné omezené podmnožině reálných čísel.

Pro další příklady viz Řešené příklady - Řady funkcí.

Konvergence řad funkcí
Zpět na Přehled metod - Řady funkcí