Konvergence řad funkcí: Přehled metod

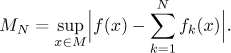
Je dána řada funkcí ∑ f_k(x) a předpokládáme, že průnik všech jejich definičních oborů není prázdný. Obvykle se ptáme na dvě věci: Jaký je obor (absolutní) konvergence a zda alespoň někde řada konverguje stejnoměrně.

Otázka 1: Vyšetřete (bodovou) konvergenci a absolutní konvergenci dané řady funkcí.
Řešení: Absolutní konvergence: Uvažujte obecné x z průniku definičních oborů, vezměte jej jako pevný parametr a otestujte konvergenci řady reálných čísel ∑ | f_k(x)|. Všimněte si, že členy této řady jsou všechny nezáporné, takže lze použít všechny ty báječné testy. Odpověď (konverguje, diverguje) ve většině případů závisí na hodnotě parametru x. Obor absolutní konvergence je množina všech x, pro která řada s absolutními hodnotami konverguje.
Konvergence: Uvažujte obecné x z průniku definičních oborů, vezměte jej jako pevný parametr a otestujte konvergenci řady reálných čísel ∑ f_k(x). Odpověď (konverguje, diverguje) ve většině případů závisí na hodnotě parametru x. Obor konvergence je množina všech x, pro která tato řada konverguje. Všimněte si, že členy ted nemusí být nezáporné, výsledná řada často ani není alternující, takže obor konvergence se obvykle hledá poněkud hůře než obor absolutní konvergence.

Otázka 2: Vyšetřete stejnoměrnou konvergenci dané řady funkcí.
Řešení: Nejprve zvolte rozumného kandidáta na množinu stejnoměrné konvergence M, a to nějakou podmnožinu oboru konvergence. V typickém případě nedostaneme stejnoměrnou konvergenci na celém oboru konvergence, ale můžeme ji dostat, pokud odstraníme malá okolí krajních bodů tohoto oboru konvergence, často je také potřeba odříznout neomezené části. Velmi často máme stejnoměrnou konvergenci na libovolném omezeném uzavřeném intervalu, který je podmnožinou oboru konvergence.
Když už se zvolila nadějná množina M, jak rozhodnete, zda je na ní stejnoměrná konvergence? Ve velmi vzácných případech je znám součet řady f. Pak spočítejte

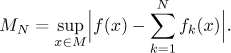
Jestliže jde M_N k nule pro N jdoucí do nekonečna, pak je stejnoměrná konvergence na M dokázána.

V prakticky všech případech ale není součet f znám. Pak nejčastěji používáme Weierstrassovu větu.

Krok 2. Vyšetřete řadu ∑ a_k (reálných nezáporných čísel). Jestliže tato řada konverguje, pak řada funkcí ∑ f_k konverguje stejnoměrně na M.

Poznámka: Někdy se jako a_k dají vzít čísla větší než ona suprema, aby si člověk usnadnil vyšetřování výsledné řady, viz způsob, kterým je Weierstrassovo kritérium formulováno. Všimněte si také, že zkoumání suprem f_k může napovědět při tipování správné M. Když zkoumáme suprema přes celý obor konvergence a výsledné a_k tvoří divergentní řadu, pak často pomůže položit si otázku: Která část oboru způsobila, že jsou tyto a_k příliš velké?

Weierstrassovo kritérium je docela silné a je to obvykle první volba metody, ale není všemocné. Pak je dobré znát nějaké alternativy, například Dirichletovo kritérium nebo Abelovo kritérium, viz sekci Řady funkcí v části Teorie - Řady funkcí.

Příklad: Vyšetřete konvergenci řady

Protože je číslo k^x kladné pro libovolné reálné x a každé přirozené číslo k, konvergence a absolutní konvergence souhlasí. Jestliže je x pevně zvolené číslo, pak není třeba hledat nějaké testy, jde o typickou p-řadu (zde p = x), jejíž konvergenci si pamatujeme. Proto víme, že tato řada konverguje (a konverguje absolutně), přesně když x > 1.
Závěr: Obor (absolutní) konvergence je interval (1,∞).

Víme, že se konvergence p-řady zlepšuje s rostoucím p (v našem případě s rostoucím x), ale zhoršuje se, když se blížíme s parametrem k 1. Máme tedy podezření, že oblast okolo 1 bude kazit stejnoměrnou konvergenci. Protože neznáme součet dané řady (kromě několika speciálních hodnot x), uchýlíme se k Weierstrassovu kritériu. Nejprve se podíváme, jestli bychom nedostali stejnoměrnou konvergenci na celém oboru konvergence M = (1,∞). Dostaneme

Řada ∑ a_k, kterou tímto způsobem dostaneme, je slavná harmonická řada, o které víme, že je divergentní. Weierstrassovo kritérium tedy selhalo, což jsme vlastně očekávali.

Zkusíme to znovu, tentokráte s menší množinou M. Rozhodneme se testovat stejnoměrnou konvergenci pro interval M = ⟨a,∞) pro nějaké libovolně zvolené a > 1. Teď máme

Pak

a protože a bylo zvoleno větší než 1, podle p-testu tato řada konverguje. Tím jsou Weierstrassovy předpoklady splněny a dostáváme stejnoměrnou konvergenci.
Závěr: Daná řada konverguje stejnoměrně na množinách M = ⟨a,∞) pro libovolné a > 1.

Pro další příklady viz Řešené příklady - Řady funkcí.

Úpravy (mocninných) řad
Zpět na Přehled metod - Řady funkcí