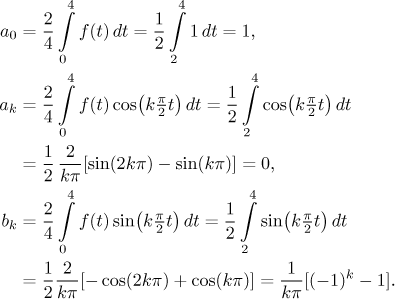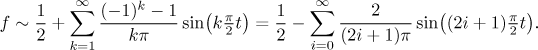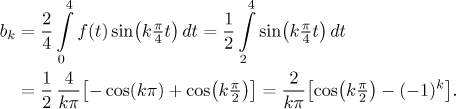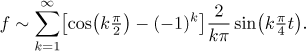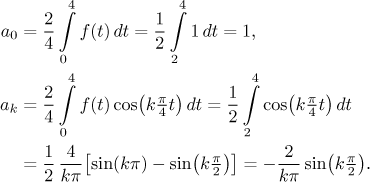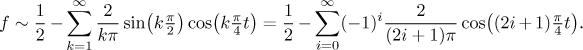Rozvoj v (sinovou, kosinovou) Fourierovu řadu: Přehled metod

Otázka: Najděte Fourierovu řadu pro funkci f (t), která je buď T-periodická nebo zadána na nějakém intervalu typu ⟨a,a + T ). Najděte součet této řady.

Řešení: Nejprve určete frekvenci ω = 2π/T a pak najděte koeficienty vypočtením integrálů

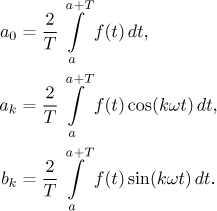
Fourierova řada se pak získá jako

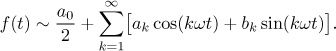
Pokud je f dostatečně pěkná (viz Jordanovy podmínky), můžete určit součet výsledné Fourierovy řady. Nejprve nakreslete T-periodickou funkci f (buď tak byla zadána, nebo byla dána na vhodném intervalu, pak nakreslete její periodické rozšíření). Potom v každém bodě nespojitosti zakreslete body na úrovních, které jsou průměrem hodnot zleva a zprava v tomto bodě. Toto je součet oné Fourierovy řady.

Poznámka: Koeficient a₀ je ve skutečnosti dán stejným vzorcem jako ostatní a_k, takže jsme mohli uvést jen jeden vzorec. Pro k = 0 se ale kosinus stane jedničkou a v praxi proto stejně počítáme a₀ zvlášť. Je proto pohodlné si to vydělit coby speciální případ.

Otázka: Najděte sinovou Fourierovu řadu pro funkci f (t), která je zadána na nějakém intervalu typu ⟨0,L ). Najděte součet této řady.

Řešení: Sinová řada je založena na lichém rozšíření s periodou T = 2L. Nejprve určete frekvenci ω = 2π/T = π/L. Pak najděte koeficienty b_k jako předtím, ale s L namísto T, položte a₀ a a_k rovné nule a napište řadu přesně jako předtím.

Pokud je f dostatečně pěkná (viz Jordanovy podmínky), můžete určit součet výsledné Fourierovy řady. Nejprve nakreslete danou funkci. Poté rozšiřte tento graf také na interval (−L,0) takovým způsobem, aby byla výsledná funkce lichá (překlopte graf okolo obou os). Pak nakreslete T = 2L-periodické rozšíření této liché funkce a zpracujte body nespojitosti přesně jako předtím.

Otázka: Najděte kosinovou Fourierovu řadu pro funkci f (t), která zadána na nějakém intervalu typu ⟨0,L ). Najděte součet této řady.

Řešení: Kosinová řada je založena na lichém rozšíření s periodou T = 2L. Nejprve určete frekvenci ω = 2π/T = π/L. Pak najděte koeficienty a₀ a a_k jako předtím, ale s L namísto T, položte b_k rovny nule a napište řadu přesně jako předtím.

Pokud je f dostatečně pěkná (viz Jordanovy podmínky), můžete určit součet výsledné Fourierovy řady. Nejprve nakreslete danou funkci. Poté rozšiřte tento graf také na interval (−L,0) takovým způsobem, aby byla výsledná funkce sudá (překlopte graf okolo osy y). Pak nakreslete T = 2L-periodické rozšíření této sudé funkce a zpracujte body nespojitosti přesně jako předtím.

Často je možné výslednou řadu vylepšit pomocí následujících užitečných vzorců.

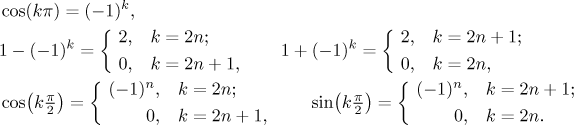
Příklad: Najděte Fourierovu řadu, sinovou Fourierovu řadu a kosinovou Fourierovu řadu pro funkci

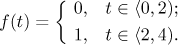
Tuto funkci lze rozšířit na funkci s periodou T = 4, frekvence je tedy ω = π/2. Najdeme koeficienty:

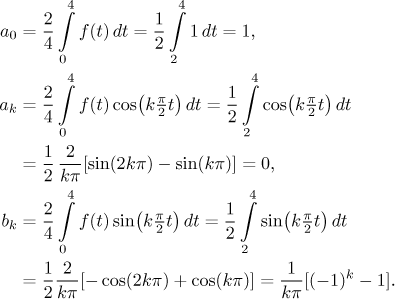
Dostaneme tedy řadu

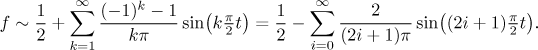
Všimli jsme si, že v řadě jsou sudé koeficienty rovny nule a liché jsou rovny −2, takže jsme řadu přepsali příslušným způsobem.

Sinová a kosinová řada mají L = 4, T = 8 a ω = π/4. Sinová řada má a_k = 0 a

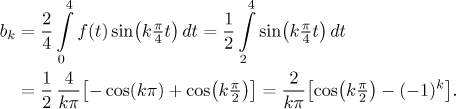
Sinová Fourierova řada tedy je

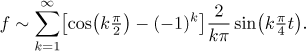
Kosinová Fourierova řada má b_k = 0 a

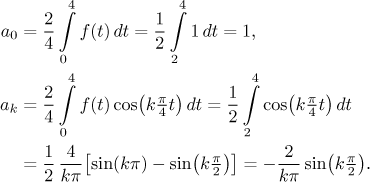
Kosinová Fourierova řada tedy je

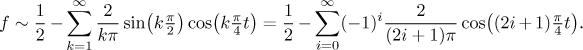
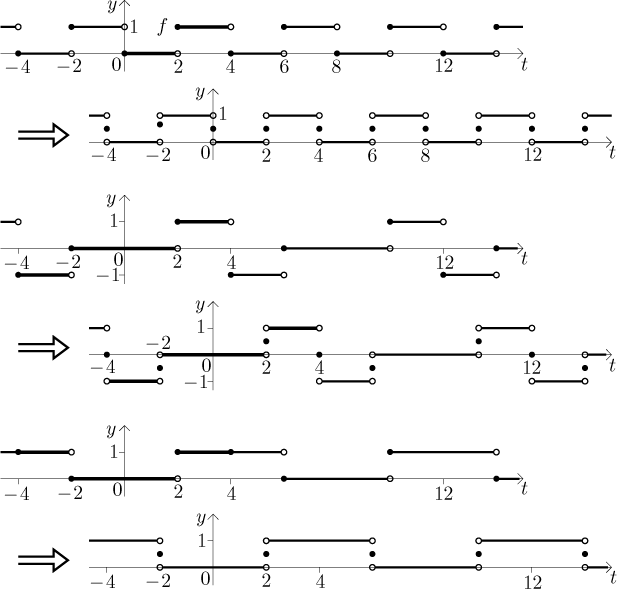
Teď určíme součty těchto tří řad. Na následujícím obrázku vidíme šest grafů. První je periodické rozšíření dané funkce a druhý je součet Fourierovy řady podle Jordanových podmínek. Třetí graf je liché periodické rozšíření a pak je tam součet sinové Fourierovy řady. A konečně na pátém grafu je sudé periodické rozšíření a pak je tam součet kosinové Fourierovy řady.

Všimněte si, že ta Fourierova řada má tvar 1/2 plus sinová řada. Pokud totiž vezmeme periodické rozšíření f a posuneme jej dolů o 1/2, dostaneme lichou funkci, jejíž Fourierova řada nutně obsahuje jen siny (je tedy také její sinovou Fourierovou řadou).

Zpět na Přehled metod - Řady funkcí
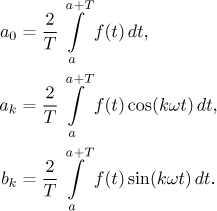
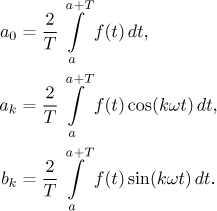
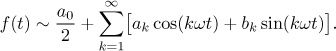
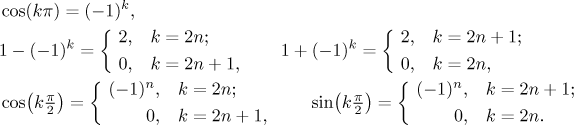