Fourierovy řady

Zde představíme trigonometrické řady a prozkoumáme možnost vyjádřit funkce pomocí takových řad. Nejprve budeme pracovat na celé reálné ose a uvedeme teorii stojící za Fourierovými řadami. Pak tuto teorii aplikujeme na funkce na intervalech a uvedeme pojem sinové a kosinové Fourierovy řady.

Základní myšlenka Fourierových řad je zjistit, co se dá udělat se siny a kosiny. Ty přirozeně žijí na intervalu ⟨0,2π⟩, my ale budeme chtít pracovat na intervalu ⟨0,T ⟩ pro nějaké T > 0 a uvažovat všechny siny a kosiny, jejichž periody jsou zlomky tohoto T, protože pak na ten interval pěkně pasují (viz tato poznámka). Je dobrý nápad si pod T představit vlnovou délku, siny a kosiny se pak musí stlačit pomocí příslušné frekvence ω dané obvyklým vzorečkem známým z fyziky, ω = 2π/T. Budeme teď uvažovat systém funkcí {sin(kωt), cos(kωt)}, kde k jsou celá čísla, je to takzvaný trigonometrický systém. Rádi bychom věděli, které funkce lze vyjádřit pomocí tohoto systému (viz sekce Systémy funkcí). Než se na tuto otázku podíváme, budeme zkoumat systém samotný.

Za prvé, jaké hodnoty k máme v onom systému? Připomeňme (viz Systémy funkcí), že chceme maximální vysledek s co nejmenší množinou, takže rozhodně chceme lineárně nezávislou množinu. Protože siny jsou liché a kosiny jsou sudé, neměli bychom v tom systému používat pro k záporná celá čísla, protože tím bychom jen zdvojovali funkce, které už tam jsou, a tak zkazili nezávislost. Jestliže k = 0, pak sinová funkce dává sin(0) = 0, což by zase zkazilo nezávislost. Na druhou stranu, cos(0) = 1 a není důvod tuto funkci vylučovat, ona přispívá k prostoru funkcí, ke kterým se lze dostat. Když tedy říkáme trigonometrický systém, tak tím opravdu míníme množinu funkcí

{1, sin(kωt), cos(kωt) pro přirozená čísla k}.

Poznamenejme, že ve skutečnosti je trigonometrických systémů hodně, odpovídají různým volbám T. Nemícháme je dohromady, takže když mluvíme o trigonometrickém systému, vždy se předpokládá, že je to systém odpovídající nějakému pevně zvolenému T (a odpovídající frekvenci omega).

Když jsme si toto vyjasnili, tak už je snadardní fakt, že siny a kosiny v trigonometrickém systému tvoří lineárně nezávislou množinu. Je ale ještě hlubší způsob, kterým jsou tyto funkce různé. V mnoha oblastech matematiky se používá následující kritérium toho, jak jsou funkce navzájem vzdáleny. Jsou-li dány dvě funkce f a g na intervalu I, tak je vynásobíme a tento součin integrujeme přes I. Čím větší je výsledné číslo (v absolutní hodnotě), tím víc mají ony funkce společného. Největší nezávislost pak evidentně nastane, když je integrál nulový, to odpovídá kolmosti vektorů. A přesně to se děje pro dvě různé funkce z našeho systému.

Fakt.
Nechť T > 0, označme ω = 2π/T.
Pro všechna celá čísla m,n > 0 platí následující.

Existuje ještě jedna funkce v našem trigonometrickém systému, konstantní funkce cos(0) = 1. Také tato funkce je v tomto smyslu kolmá ke všem ostatním funkcím trigonometrického systému, ale je výjimečná v jednom ohledu. Ty vzorce ve Faktu mimo jiné říkají, že když integrujeme druhé mocniny sinů a kosinů přes základní interval ⟨0,T ⟩, tak dostaneme T /2. Když ale integrujeme druhou mocninu cos(0), tak dostaneme T. To ukazuje, že tato funkce je trochu jiná a proto se s ní také bude trochu jinak zacházet, jak uvidíme v následující definici.

Ona vlastnost kolmosti dělá z trigonometrického systému něco velmi speciálního a silně se to hodí, když se začneme ptát na jednu ze základních otázek této sekce: Jak vyjádříme jiné funkce pomocí trigonometrických funkcí? Když vyjadřujeme funkce pomocí tohoto systému, tak jsou počátečním bodem tradiční lineární kombinace funkcí z trigonometrického systému, ale hlavním předmětem zájmu budou "nekonečné lineární kombinace" - tedy řady. Existuje mnoho způsobů, kterým mohou být sinu a kosiny uspořádány a seřazeny, ale jeden se ukázal jako nejpraktičtější; teď tedy představíme formy, které budeme dále používat.

Definice.
Nechť T > 0, označme ω = 2π/T.
Pojmem trigonometrický polynom stupně N rozumíme funkce

Pojmem trigonometrická řada rozumíme funkční řady

kde a_k a b_k jsou reálná čísla.

Které funkce lze vyjádřit jako řadu tohoto typu? Jako obvykle jde o velice obtížnou otázku a my použijeme tradiční přístup. Budeme předpokládat, že nějaká funkce f už byla vyjádřena jako taková řada, a pak zkusíme zjistit, co to pro tuto f a pro řadu znamená.

Začneme něčím jednoduchým. Všimněte si, že všechny funkce v trigonometrickém systému jsou T-periodické, takže automaticky také všechny lineární kombinace T_N(t) jsou T-periodické. Přechodem k limitě dostaneme, že také trigonometrické řady (když konvergují) jsou T-periodické. To nám hned dává následující pozorování.

Fakt.
Nechť T > 0, označme ω = 2π/T. Předpokládejme, že pro všechna reálná čísla t máme

Pak je f nutně T-periodická.

Proto jestliže chceme vyjádřit funkci f pomocí trigonometrické řady, tak nemá smysl zkoušet jiné funkce než ty periodické. Proto také stačí dělat naše úvahy jen na intervalu ⟨0,T ⟩ (nebo nějakém jeho posunu). Bohužel, nejsou žádná další užitečná pozorování, která lze relativně snadno udělat z předpokladu, že je naše funkce vyjádřena jako trigonometrická řada. Pokud chceme víc, musíme také předpokládat víc, jmenovitě stejnoměrnou konvergenci této řady.

Věta (jednoznačnost).
Nechť T > 0, označme ω = 2π/T. Předpokládejme, že f je T-periodická funkce taková, že pro všechna reálná čísla t máme

Předpokládejme dále, že konvergence této řady je stejnoměrná na ⟨0,T ⟩. Pak jsou koefficienty této řady nutně dány vzorci

Všimněte si, že také a₀ je vlastně dáno druhým vzorcem, protože pro k = 0 je kosinus v tomto integrálu vždy 1. Je nicméně tradiční formulovat to tímto způsobem, protože i kdybychom to napsali jako jeden vzoreček, stejně bychom při praktickém výpočtu museli řešit dva případy; konec konců, jak už jsme viděli, ta funkce 1 je trochu speciální.

Větu jsme nazvali "věta o jednoznačnosti", protože říká, že periodickou funkci lze vyjádřit jako trigonometrickou řadu jen jedním způsobem. Všimněte si ovšem, že tuto jedinečnost máme jen pro případ, kdy řada konverguje stejnoměrně. Jinak se může stát, že funkci lze vyjádřit jako trigonometrickou řadu a tato řada není ta z věty výše. To je docela rozdíl ve srovnání s chováním mocninných řad. Podstata rozdílu je v tom, že pro mocninné řady konvergence implikovala stejnoměrnou konvergenci (na téměř celém oboru konvergence), čímž se dostala ta jednoznačnost vždy. Tady se může stát (a často tomu tak je), že máme konvergenci, která stejnoměrná není.

Všimněte si také, že se tato jednoznačnost vztahuje pouze na řady, jejíž základní perioda je T. Pokud je funkce f také S-periodická, tak můžeme dostat jiný rozvoj.

Teď už víme, že když chceme rozvinout funkci pomocí trigonometrické řady, tak jediná cesta, která má naději na úspěch, je použít ty koeficienty z věty. Abychom to mohli udělat, musíme nějak zajistit, že ty integrály existují. (V té větě jsme se o to nemuseli bát, protože stejnoměrná konvergence řady, jejíž členy jsou spojité, dává spojitou - a tudíž integrovatelnou - funkci.)

Definice.
Nechť f je T-periodická funkce pro nějaké T > 0, označme ω = 2π/T. Předpokládejme, že f je Riemannovsky integrovatelná na ⟨0,T ⟩.
Definujeme Fourierovu řadu funkce f jako řadu

kde koeficienty jsou dány vzorcem

Všimněte si, že toto je čietě formální přiřazení. Je-li dána f, tak spočítáme ty integrály a vytvoříme řadu, ale není zaručeno, že tato řada opravdu konverguje, a pokud ano, tak že konverguje k f. Toto formální přiřazení zapíšeme následovně.

Co dobrého se dá od takové řady očekávat? Konvergence Fourierových řad je velice choulostivá a obtížná oblast, matematici na tom pracují už přes sto let. Je jasné, že zde v Math Tutoru jsme daleko od úrovně potřebné k porozumění tomu všemu, takže jen ukážeme několik užitečných výsledků. Pro začátek poznamenáme, že i když je f spojitá, tak k ní ještě její Fourierova řada nemusí konvergovat; v typickém případě dokonce nebude, často dokonce ani nekonverguje v mnoha bodech. To nezní moc slibně. Z praktického pohledu ale některé nadějné výsledky máme. Ukazují, že kvůli konvergenci se na f musíme podívat hlouběji, ale pak nám na druhou stranu nevadí nějaká malá nespojitost tam či onde.

Věta (Dirichlet).
Nechť f je T-periodická funkce pro nějaké T > 0, označme ω = 2π/T. Předpokládejme, že f je Riemannovsky integrovatelná na ⟨0,T ⟩. Nechť

Předpokládejme, že f je diferencovatelná na nějakém prstencovém okolí nějakého bodu t₀ a že tato derivace má jednostranné limity v t₀. Pak Fourierova řada funkce f konverguje v t₀ a

Připomeňme, že f (t₀⁺) značí limitu zprava v t₀, f (t₀^-) značí limitu zleva v t₀,

Tato věta má tři důležité aspekty. Za prvé, konvergenci Fourierovy řady lze odvodit z diferencovatelnosti, což se často používá. Za druhé, tato konvergence (a hodnota této limity) záleží jen na chování f okolo bodu t₀. To znamená, že na chování Fourierovy řady v t₀ nemá vliv, jak f vypadá dále od tohoto bodu. Výsledkům tohoto typu se říká princip lokalizace.

Znamená to také, že samotná hodnota f v t₀ je irelevantní. Ona se totiž opravdu vůbec v té větě neobjeví, dokonce ani nepřímo, a vlastně by to nemělo překvapit. Protože jsou koeficienty Fourierovy řady dány jako integrály, tak to znamená, že danou funkci můžeme změnit v konečně mnoha bodech, aniž bychom změnili výslednou řadu.

Třetí důležitý aspekt je, že Fourierova řada nevrací přímo původní funkci, ale jakýsi její průměr. Je-li dáno t₀ jako ve větě, pak se Fourierova řada podívá trochu doleva a trochu doprava a vybere si přesně prostřední hodnotu.

Jak jsme viděli, Fourierova řada nedává přesně hodnotu funkce, ale její limitu. V praxi bychom ovšem ocenili, kdybychom měli skutečnou rovnost mezi f a její Fourierovou řadou. Je jen jeden způsob, jak toho dosáhnout, musíme přinutit hodnotu funkce, aby se rovnala jednostranným limitám - a to znamená spojitost.

Věta.
Nechť f je T-periodická funkce pro nějaké T > 0, označme ω = 2π/T. Předpokládejme, že f je Riemannovsky integrovatelná na ⟨0,T ⟩. Nechť

Jestliže je f diferencovatelná v nějakém t₀, pak

Teď se podíváme na globální situaci. Nebudeme vyžadovat spojitost všude (protože Fourierovy řady jsou obzvláště zajímavé pro nespojité funkce), ale abychom dostali něco rozumného, nemůžeme funkci dovolit příliš mnoho problémů. Jedna možnost je udělat to následovně. Chceme, aby se funkce skládala z "pěkných" úseků, na každém z nich očekáváme, že funkce bude spojitá a případně i jinak příjemná. V krajních bodech každého úseku budeme chtít konvergentní jednostranné limity. Pro přesnější definici viz například tato poznámka. Klíčovou vlastností je tzv. konečná variace, konvergenci Fourierových řad pak zaručuje Jordanova věta. Bohužel, zjišťovat konečnou variaci není snadné, proto se v praxi raději díváme na silnější, nicméně snadnější vlastnosti. Jedna užitečná verze může být tato.

Připomeňme, že význam pojmu po částech spojité a diferencovatelné funkce je následující: Její definiční obor (v tomto případě reálná osa) lze rozdělit na intervaly (v našem případě nekonečně mnoho), jejichž délky se nestávají libovolně malé, a na vnitřku každého z těchto intervalů je funkce spojitá, diferencovatelná, derivace je spojitá, a funkce i její derivace mají vlastní jednostranné limity v krajních bodech těchto intervalů. Jako příklad na obrázku uvádíme nejprve typickou funkci splňující předpoklady věty a poté jak by vypadal součet její Fourierovy řady.

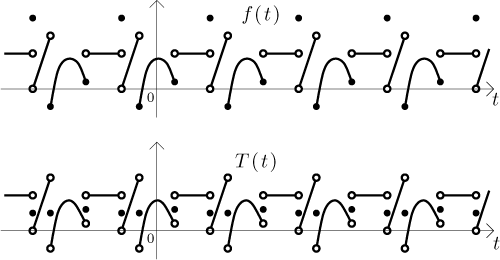
Jak vidíme, řada na spojitých úsecích vrací původní funkci, ale v bodech nespojitosti vrací průměr levé a pravé limity, ať už je hodnota přímo v těch bodech jakákoliv. Pro "opravdický" příklad, s funkcí danou vzorečkem a výpočty, viz níže.

Tyto podmínky jsou velmi užitečné, nicméně občas příliš svazující, například je nelze aplikovat na funkce zahrnující odmocninu s neomezenou derivací zprava v počátku. Další užitečná verze podmínek používá monotonii po částech.

Věta (Dirichlet).
Nechť f je T-periodická funkce, která je omezená a po částech monotonní. Označme ω = 2π/T. Nechť

Pak pro každé t máme

I tuto větu bychom mohli aplikovat na obázek výše, jen bychom museli při dělení definičního oboru na intervaly monotonie rozpůlit ty, na kterých měla funkce tvar kopečku, zatímco předchozí věta je zvládla vcelku.

Poznamenejme, že zatímco pro spojité funkce máme stejnoměrnou konvergenci (což je velice žádoucí), tak není šance to dostat pro funkce nespojité. Abychom viděli, co se děje, představíme si velice jednoduchou funkci s nespojitostí, funkci f identicky rovnou 0 pro x z (−1,0) a identicky rovnou 1 pro x z (0,1), tento vzor se pak periodicky opakuje (viz obrázek níže). Zajímá nás, co se bude dít v 0. Všimněte si, že jsme nespecifikovali hodnoty v 0,1,−1,2,... protože víme, že na Fourierovu řadu stejně nebudou mít žádný vliv.

Částečné součty odpovídající Fourierovy řady se snaží dobře aproximovat f, a protože je f spojitá a spojitě diferencovatelná na (−1,0), Fourierova řada tam musí konvergovat k 0. Podobně musí konvergovat k 1 na (0,1). Co se děje okolo nespojitosti v x = 0? Částečné součty Fourierovy řady se musí velice rychle změnit z hodnot okolo 0 na hodnoty okolo 1. Jak tak skáčou z jedné úrovně na druhou, tak vypadá přirozeně, že se v x = 0 dostanou nahoru do poloviny cesty, takže by hodnota měla být 1/2. Zdálo by se tedy, že to průměrování, které jsme diskutovali, se vlastně dá čekat.

Navíc částečné součty coby spojité funkce nemohou skákat z 0 do 1 okamžitě, ten skok zabere nějaké místo (na ose x), jinými slovy, konkrétní částečný součet (když si jej prohlížíme zleva doprava) musí opustit úroveň 0 už předtím, než je x rovno 0, a pro x záporné ale hodně blízké 0 je tento částečný součet téměř 1/2, zatímco funkce f je pořád ještě 0. Globální kvalita aproximace tedy nemůže být lepší než tento rozdíl 1/2 a globální stejnoměrná konvergence je nemožná.

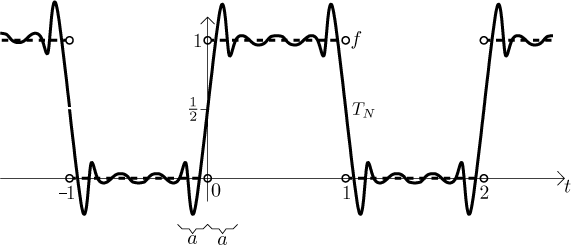
Poznamenejme, že máme stejnoměrnou konvergenci na libovolném intervalu, který neobsahuje body nespojitosti. To také znamená, že když si vezmeme libovolné velmi malé a > 0, tak je konvergence stejnoměrná na ⟨−1/2,−a⟩ a tudíž částečné součty T_N s velkým N musí začít své stoupání na úroveň 1 až po opuštění tohoto intervalu, tedy až po -a, a z analogického důvodu už musí být skoro 1 po a. Jinými slovy, ty rychlé změny z úrovně 0 na úroveň 1 se dějí v rámci velice úzké oblasti okolo počátku a tato oblast se zmenšuje víc a víc jak N roste. Částečné součty proto musí v tomto bodě nespojitosti spěchat stále více. Tím se vytváří jeden zajímavý prvek Fourierových řad.

Jak ty částečné součty spěchají nahoru, tak přestřelí a vylezou výrazně nad 1, teprve pak se usadí. Můžeme tu situaci také číst zprava doleva, částečné součty pak rychle klesají a přestřelí i nalevo. Toto chování se stane vždy, když se Furoerova řada musí vypořádat s nespojitostí. Na obou jejích stranách se u částečných součtů objevují oscilace, které jsou na stále užším a užším prostoru, ale jejich velikost se nezmenšuje. Tato porucha se jmenuje Gibbsův jev a můžete ji vidět na skutečném příkladě v této poznámce.

Tuto část uzavřeme několika jednoduchými pozorovnáními. První a důležité je, že protože jsou všechny funkce vystupující v úvahách T-periodické, tak není důvod preferovat interval ⟨0,T ⟩. Libovolný jeho posun bude také fungovat, takže jsme ve všech předchozích větách mohli také použít například následující předpoklad: "Nechť f je funkce, která je Riemannovsky integrovatelná na nějakém intervalu typu ⟨a,a + T )." Především to platí o vzorcích pro koeficienty Fourierovy řady. To je někdy užitečné, rozhodně to stojí za to vyjádřit formálně.

Fakt.
Nechť f je T-periodická funkce pro nějaké T > 0, označme ω = 2π/T. Předpokládejme, že f je Riemannovsky integrovatelná na intervalu ⟨a,a + T ⟩ pro nějaké reálné číslo a. Pak jsou koeficienty její Fourierovy řady dány vzorcem

Jedna populární volba je integrovat přes interval od -T /2 do T /2. Pak je integrační interval symetrický kolem počátku, všimněte si, že i siny a kosiny v těch integrálech jsou symetrické funkce (siny jsou liché, kosiny sudé), takže pokud máme nějakou symetrii také pro funkci f, může nám to velice zjednodušit situaci. Pomocí pravidel pro násobení symetrických funkcí (viz Funkce - Teorie - Reálné funkce - Základní vlastnosti) a základních vlastností integrálů (viz Integrály - Teorie - Úvod - Vlastnosti Riemannova integrálu) okamžitě dostáváme následující.

Krátce, liché funkce dávají sinové řady a sudé funkce dávají kosinové řady. To se nám bude hodit později, viz sinová a kosinová Fourierova řada.

Funkce na intervalech

Právě jsme viděli, že k vytvoření Fourierovy řady nám vlastně stačí znát funkci f na nějakém intervalu typu ⟨a,a + T ⟩. To nám dává příležitost silně zobecnit Fourierovy řady, protože když máme funkci definovanou na takovém intervalu, můžeme z ní snadno udělat T-periodickou funkci definovanou na celé reálné ose prostě tak, že "opakujeme daný vzor." Je tady potřeba trochu opatrnosti, protože koncový bod a + T daného intervalu je také počátečním bodem následujícího intervalu, takže by tam hodnota f měla být stejná jako hodnota v a. Protože to se pro obecnou funkci definovanou na ⟨a,a + T ⟩ nedá zaručit, tak prostě ten pravý krajní bod vynecháme ze základního intervalu. Všimněte si, že libovolný interval typu ⟨a,b) lze napsat jako ⟨a,a + T ). Vlastně bychom také mohli vynechat levý krajní bod nebo oba a na výslednou Fourierovu řadu by to nemělo vliv; jak už jsme viděli, změnou funkce v jednom bodě (a jeho periodických posunech) vůbec Fourierovu řadu neovlivníme. Volba ⟨a,b) je tradiční.

Definice.
Nechť f je funkce definovaná na nějakém intervalu ve tvaru ⟨a,a + T ). Definujeme její periodické rozšíření jako funkci f definovanou na celé reálné ose vzorcem

Všimněte si, že v definici je trochu zmatek. To f napravo je původní f definované pouze na daném intervalu, zatímco f nalevo je ta nová funkce definovaná na reálné ose. Protože se tyto funkce shodují v místech, kde jsou obě definovány, je zvykem používat jedno pímenko pro obě, i když to v té definici může vypadat srandovně.

Teď už můžeme vytvořit Fourierovu řadu také pro funkce definované na nějakém konečném intervalu.

Definice.
Nechť f je funkce definovaná na nějakém intervalu ve tvaru ⟨a,a + T ). Předpokládejme, že je tam Riemannovsky integrovatelná. Definujeme její Fourierovu řadu jako Fourierovu řadu jejího periodického rozšíření.

Všimněte si, že formálně dostaneme Fourierovu řadu definovanou na celé reálné ose, ale protože f bylo původně definováno jen na jistém intervalu I, tak nás obvykle zajímá, jen co řada dělá tam. Jak ale uvidíme níže, abychom to viděli, tak se budeme muset také rozhlédnout kolem, na periodické rozšíření.

Příklad: Odvodíme Fourierovu řadu pro funkci

Tato funkce je spojitá, tudíž integrovatelná. Když ji rozšíříme periodicky, dostaneme 2-periodickou funkci (protože délka základního intervalu je 2). Frekvence je tedy ω = π. Teď vypočítáme příslušné integrály, v případě potřeby pomocí integrace per partes.

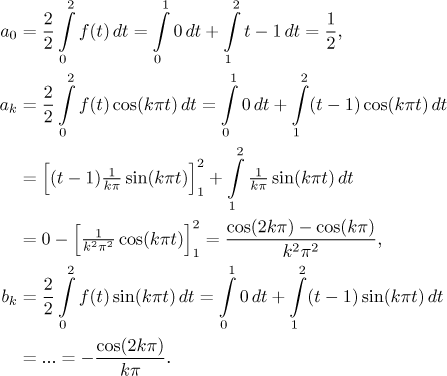
Jsme připraveni sestavit příslušnou trigonometrickou řadu. Aby vypadala lépe, tak si připomeneme, že cos(2kπ) = 1, a velice užitečný fakt, že cos(kπ) = (−1)^k. Když toto použijeme ve vzorci pro a_k, pak bude čitatel buď 0 (když je k sudé) nebo 2 (pro k liché). To nám nabízí příležitost dále výslednou řadu zjednodušit tím, že zavedeme index n a použijeme k = 2n + 1, což je známý trik pro zápis všech lichých přirozených čísel. Není nutné to dělat, ale je pěkné odpovědět způsobem, který jasně ukáže, co se vlastně děje, takže si to čtenář nemusí sám přelouskávat.

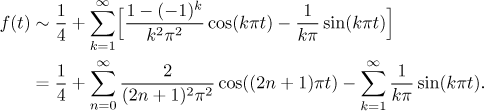
Co má tato řada společného s danou funkcí f? Fourierovu řadu jsme přiřadili k periodickému rozšíření dané f, takže bychom měli začít tím, že si to rozšíření představíme (viz první graf v obrázku níže). Můžeme k určení součtu naší řady použít Jordanovy věty? Z obrázku vidíme, že se peroodické rozšíření skládá z úseků, na kterých je f přímka, takže je na těch úsecích spojitá a difrencovatelná, s konvergentními limitami (jak f tak f ′) v krajních bodech. Konec konců, v definici máme jen vzorce, které jsou spojité a spojitě diferencovatelné s limitami v koncových bodech, což je něco, co se nedá zkazit periodickým rozšířením.

Každopádně lze aplikovat onu Větu a řada se tedy chová následovně. Funkce f je spojitá ve všech bodech intervalu (0,2) a jeho posunů o 2, takže tam bude řada konvergovat k f. Zbývá tedy zjistit, co se děje v bodě 2 a jeho posunech o 2. Vidíme, že limita f v 2 zleva je 1; na druhou stranu limita v 2 zprava je (díky periodicitě) stejná jako limita f v 0 zprava, tedy 0. Průměr je 1/2. Tak získáme součet řady, jak ukázán druhým grafem v následujícím obrázku.

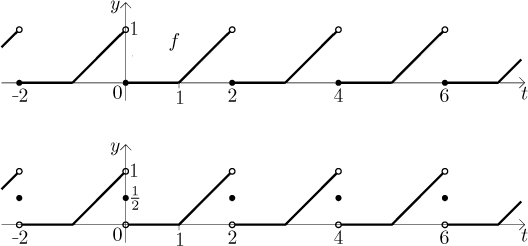
Toto je obvykle považováno za dostatečnou odpověď na následující otázku: "Co je součtem výsledné Fourierovy řady?" Pro více detailů o konvergenci Fourierový řady v tomto příkladě se podívejte na tuto poznámku. Mimo jiné tam uvidíte animaci částečných součtů a Gibbsův jev.

Jeden z důvodů, proč je obvykle obrázek považován za dostačující, je fakt, že zapsat výsledek vzorečkem je obvykle komplikované a méně názorné. Abyste to viděli, uděláme výjimku a zapíšeme náš výsledek "pořádně", ale jen pro interval ⟨0,2). Konec konců, funkce je původně zadána jen tam, takže je přirozené se na tuto množinu soustředit.

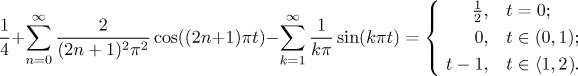
Co nám takový výsledek říká? Základní myšlenka je vyjádřit danou funkci jako součet různých oscilací, typickým příkladem může být zvukový signál, který chceme vyjádřit jako kombinaci základních harmonických zvuků. Pokud jsou jisté koeficienty a_k či b_k výrazně větší než ostatní, tak to znamená, že jsou dotyčné frekvence v daném signálu výrazné. To se dá použít pro "frekvenční analýzu", ale o takových věcech mluvíme víc v sekci o Aplikacích.

Když obecně vyjádříme funkci jako Fourierovu řadu, tak jsou v ní jak kosiny tak siny. Někdy by ale bylo užitečné, kdybychom mohli použít pouze funkce dle naší volby - buď jen siny nebo jen kosiny. V mnoha případech se to dá zařídit.

Připomeňme, že jsme dříve dokázali, že liché funkce mají Fourierovu řadu bez kosinů a sudé funkce je mají bez sinů. To ukazuje, jakým způsobem dosáhnout našeho cíle. Samozřejmě pokud je nám dána funkce na celé reálné ose, tak se musíme spoléhat a symetrii, kterou už má. Když nám je ale dána funkce jen na intervalu I délky L, pak to někdy můžeme zařídit tak, aby periodické rozšíření bylo liché nebo sudé.

Uvažujme funkci definovanou na intervalu typu ⟨a,a + L ). Chceme ji rozšířit periodicky, takže můžeme předpokládat, že tento základní interval je v takové pozici, že obsahuje počátek. Jsou dva případy. Pokud je počátek uvnitř našeho intervalu, pak tento interval (a tudíž i základní tvar f ) zasahují na obě strany od počátku a tudíž je již symetrie f dána. Ten opravdu zajímavý případ je, když je 0 levý krajní bod, tedy když je funkce definována na intervalu ⟨0,0 + L ). Pak můžeme udělat následující trik. Rozšíříme definici také na interval ⟨-L ,0) a dostaneme nový základní tvar, který má délku T = 2L. Pak tento nový základní tvar rozšíříme na T-periodickou funkci a najdeme její Fourierovu řadu.

Finta je v tom, jak děláme to prodloužení na ⟨-L ,0). Můžeme prostě otočit danou f okolo osy y, tedy nová funkce je dána jako f (−x) pro x z [−L ,0). Pak jsou nový tvar a tudíž i periodické rozšíření sudé a dostaneme kosinovou řadu. Říkáme tomu sudé periodické rozšíření funkce f. Můžeme také otočit daný tvar okolo obou os, aby byla nová funkce symetrická okolo počátku, tedy nová funkce je dána jako − f (−x) pro x z [−L ,0). Pak jsou nový základní tvar a periodické rozšíření liché a dostaneme sinovou řadu. Říkáme tomu liché periodické rozšíření funkce f. Podívejte se na příklad níže, mělo by to být jasné.

Definice.
Nechť f je funkce definovaná a integrovatelná na intervalu ⟨0,L ).
Definujeme sinovou Fourierovu řadu funkce f jako Fourierovu řadu jejího lichého periodického rozšíření.
Definujeme kosinovou Fourierovu řadu funkce f jako Fourierovu řadu jejího sudého periodického rozšíření.

Když zdvojnásobíme periodu, tak také dostaneme jinou frekvenci, ω = 2π/T = π/L. Pro sudé, respektive liché rozšíření pak aplikujeme Tvrzení o symetrických funkcích a dostaneme následující vzorce pro řady k lichému, respektive sudému periodickému rozšíření.

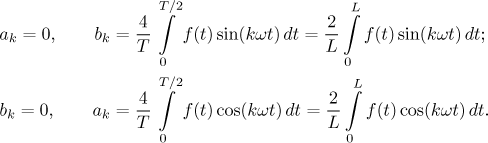
Překvapivě se až na jinou frekvenci tyto vzorce ukázaly coby stejné jako bychom dělali obvyklou Fourierovu řadu, jen namísto T použijeme L. To je docela příjemné.

Fakt.
Nechť f je funkce definovaná a integrovatelná na intervalu ⟨0,L ).
Sinová Fourierova řada pro f je trigonometrická řada s ω = π/L a koeficienty danými vzorcem

Kosinová Fourierova řada pro f je trigonometrická řada s ω = π/L a koeficienty danými vzorcem

Jestliže je f po částech spojitá s po částech spojitou derivací na ⟨0,L ), pak její sinová Fourierova řada konverguje k lichému periodickému rozšíření f modifikovanému v nespojitostech pomocí průměru.
Její kosinová Fourierova řada konverguje k sudému periodickému rozšíření f modifikovanému v nespojitostech pomocí průměru.

Příklad: Vrátíme se k předchozímu příkladu a najdeme jeho sinovou a kosinovou Fourierovu řadu. Máme L = 2, proto mají tyto dvě řady ω = π/2. Pomocí vzorců výše nejprve odvodíme sinovou Fourierovu řadu.

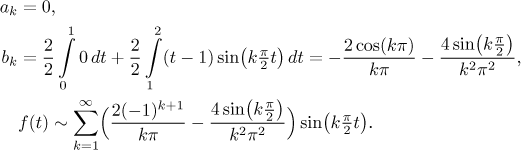
Teď odvodíme kosinovou Fourierovu řadu.

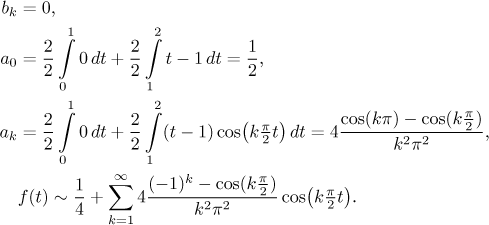
Kdybychom chtěli vědět, k jakým funkcím tyto dvě Fourierovy řady konvergují, tak musíme nejprve vytvořit liché a sudé periodické rozšíření f a pak použít tu fintu s průměrem v bodech nespojitosti. V obrázku jsme zdůraznili základní zdvojenou periodu.

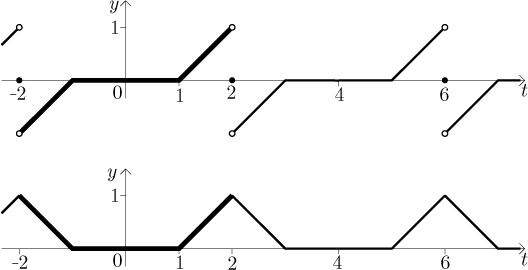
Všimněte si, že sudé periodické prodloužení je vlastně spojitá funkce, proto k ní kosinova Fourierova řada konverguje stejnoměrně. Když se přirozeně soustředíme na interval ⟨0,2), kde byla funkce původně zadána, tak vidíme, že se ty tři řady (Fourierova, sinová Fourierova a kosinová Fourierova) liší v tom, co dělají v krajních bodech daného intervalu. Zase odkazujeme na tuto poznámku pro obrázky částečných součtů.

Vlastnosti Fourierových řad
Zpět na Teorie - Řady funkcí