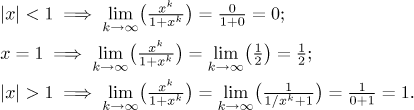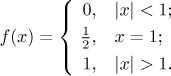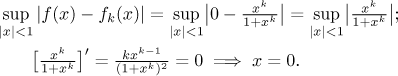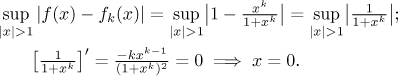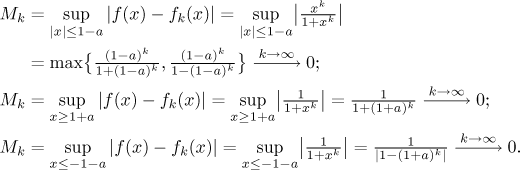Příklad: Vyšetřete konvergenci následující posloupnosti funkcí:
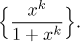
Řešení:
Než začneme, všimněte si, že bod x = −1 není v
definičních oborech funkcí s lichým k, proto jej rovnou vyřadíme ze
všech dalších úvah.
Nejprve se podíváme na bodovou konvergenci. Budeme považovat x za
parametr a spočítáme limitu vzhledem ke k. Když pošleme k do
nekonečna, tak limita xk záleží na
x, viz
geometrická
posloupnost. Musíme proto pro vyčíslení této limity použít tři rozdílné
strategie. Pro |x| < 1 členy
xk vymizí; pro
|x| > 1 se stanou dominantními a nejlepší
přístup je zbavit se jich krácením; pro
x = 1 mají všechny funkce stejnou hodnotu
a dostáváme konstantní posloupnost.
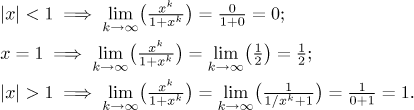
Závěr: Daná posloupnost konverguje na svém oboru konvergence,
který se skládá ze všech čísel kromě x = −1,
k funkci
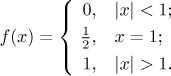
Jak je to se stejnoměrnou konvergencí? Začneme zkoumáním rozdílu mezi
f a jednou konkrétní fk na právě zjištěném
oboru konvergence. Zase musíme provádět naše zkoumání na třech oblastech. Za
prvé, v x = 1 je rozdíl vždy nulový. Pro
|x| < 1 dostaneme
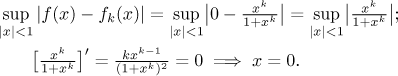
Kritický bod x = 0 je evidentně lokální
minimum dané funkce (v absolutní hodnotě), takže je supremum dáno hodnotami
v krajních bodech. Limita v 1- dává 1/2,
supremum je tedy přinejmenším 1/2 pro všechna k a tudíž
nemůžeme dostat stejnoměrnou konvergenci na
(−1,1). Všimněte si, že stejně špatné je to v −1. Jestliže je
k sudé, tak je limita v (−1)+ zase
1/2, ale jestliže je k liché, tak je tam limita dokonce
mínus nekonečno!
Stejnoměrná konvergence na celém oboru konvergence byla právě vyloučena, ale
abychom si doplnili obrázek, podíváme se ještě na dva intervaly dané
podmínkou |x| > 1.
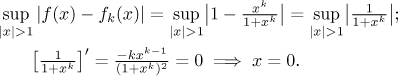
Vidíme, že výraz v supremu je rostoucí pro
x > 1 a monotonní pro
x < −1 (rostoucí když je k sudé,
klesající pro k liché). Supremum je proto dáno hodnotami v krajních
bodech. Limita v nekonečnu a mínus nekonečnu je 0, takže tam není problém.
Limita v 1+ je 1/2, takže supremum na množině dané
x > 1 je 1/2 a stejnoměrná
konvergence je tam vyloučena. A konečně také pro
x < −1 nedostaneme stejnoměrnou konvergenci,
limita (a supremum) jsou totiž buď 1/2 (pro k sudé) nebo
nekonečno (pro k liché).
Vidíme, že stejnoměrné konvergenci škodí chování dané posloupnosti na obou
stranách 1 a −1. To napovídá, že když tyto body odřízneme, pak dostaneme
stejnoměrnost. Naše pozorovnání o monotonii naznačuje, že když zvolíme nějaké
a > 0 (a aby fungoval i prostřední interval, musí být
a malé, menší než 1), pak bychom měli dostat
stejnoměrnou konvergenci na intervalech
M = (−∞,−1-a⟩,
M = ⟨−1+a,1-a⟩
a
M = ⟨1+a,∞).
Potvrdíme to vyhodnocením suprem pro tyto tři množiny.
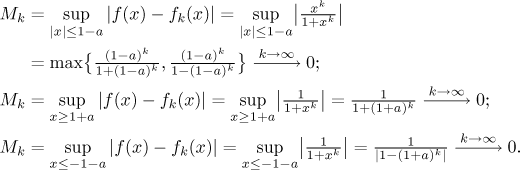
Závěr: Daná posloupnost konverguje k funkci f
stejnoměrně na množinách typu
M = (−∞,−1-a⟩,
M = ⟨1+a,∞),
M = ⟨−1+a,1-a⟩
pro libovolné a > 0
(v posledním případě také vyžadujeme a < 1).
Pro ilustraci ukážeme obrázek s některými funkcemi.
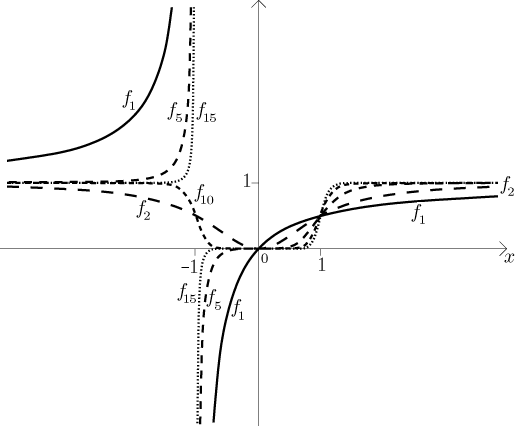
Další příklad
Zpět na Řešené příklady -
Řady funkcí
![]()