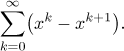
Příklad: Vyšetřete konvergenci následující řady funkcí:

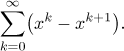
Řešení: Nejprve se podíváme na bodovou konvergenci. Budeme považovat x za parametr a vyšetříme konvergenci výsledné řady reálných čísel. V typickém případě bychom teď testovali absolutní konvergenci pomocí nějakých testů, tento přístup ukážeme v této poznámce. Takový přístup je obecnější, ale zato dává méně informace, hlavně nám neřekne, jaký je součet řady. Obvykle toto omezení akceptujeme a rovnou jdeme na testy, proč tedy ne tady?

Kdyby od nás nečekali součet této řady, jen rozhodnutí o její konvergenci, tak by nám tu řadu zadali bez limit pro index, protože ty jsou pro testování konvergence irelevantní. To, že tam ty limity jsou, je jasná nápověda. Potřebujeme tedy nějaký lepší nástroj a taky jej máme, protože daná řada je evidentně teleskopická řada. Takže dále pokračujeme tak, že vyhodnotíme částečné součty této řady a pak přejdeme k limitě vzhledem k N.

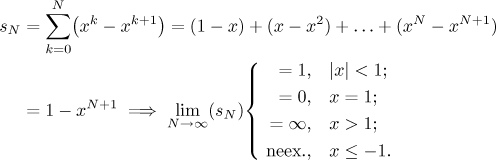
Všimněte si, že pro ty x, kde naše řada konverguje, jsou její členy nezáporné. To znamená, že právě dokázaná konvergence je také absolutní.

Závěr: Daná řada konverguje a konverguje absolutně na oboru (absolutní) konvergence (−1,1⟩ k funkci

Jak je to se stejnoměrnou konvergencí? Začneme zkoumáním rozdílu mezi f a jedním konkrétním částečným součtem s_N na právě zjištěném oboru konvergence. Protože je případ x = 1 speciální, musíme jej udělat zvlášť a hned si všimneme, že se pak jak částečné součty řady tak f rovnají 0, takže chyba aproximace je 0 a tento bod nezvětší supremum, které teď hledáme.

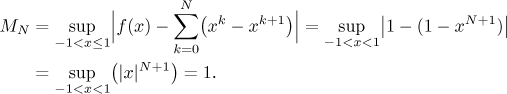
Protože toto supremum nejde k nule pro N jdoucí do nekonečna, nemáme stejnoměrnou konvergenci. Vidíme ale také, že se potíže vyskytují v 1 a −1, takže očekáváme, že když je odřízneme, dostaneme už dobré aproximace. Za tímto účelem tedy budeme uvažovat množinu typu M = ⟨-a,a⟩ pro nějaké a splňující 0 < a < 1. Pak

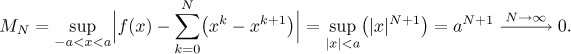
Závěr: Daná řada konverguje k funkci f stejnoměrně na množinách typu M = ⟨-a,a⟩ pro libovolné a splňující 0 < a < 1.

Další příklad
Zpět na Řešené příklady - Řady funkcí