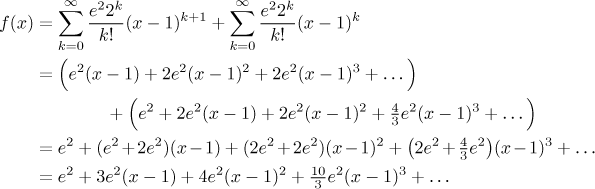Příklad: Rozviňte danou funkci v mocninnou (Taylorovu) řadu s daným středem.

Řešení: Použijeme standardní postup. Vidíme, že když rozvineme exponenciálu, tak už je hlavní práce hotova, ostatní části se udělají snadno. Daná funkce už je tedy v rozumném tvaru a můžeme přejít k prvnímu kroku, změníme všechny x tak, abychom místo nich měli výrazy (x − 1).

Pokud bychom teď rozvinuli exponenciálu, měla by výsledná řada členy jako v jejím argumentu, takže by to nebyla mocninná řada se středem 1. Potřebujeme se proto zbavit toho "+2" v exponenciále, to se snadno udělá algebraicky. Podobně se potřebujeme zbavit toho "+1" ve výrazu před exponenciálou, proto ten člen rozdělíme na dva.

Teď už jsme připraveni rozvinout tu exponenciálu pomocí řady pro e^y, pak výslednou řadu přeorganizujeme tak, aby se v ní objevily výrazy (x − 1). Také použijeme distributivní zákon a přesuneme členy, které jsou před exponenciálami, dovnitř výsledných řad.

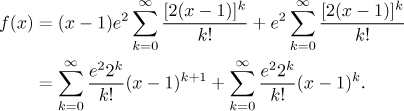
Všimněte si, že rozvoj exponenciály platí pro všechna y = 2(x − 1), z čehož plyne, že výsledek platí pro všechna x.

Máme odpověď vyjádřenu jako součet dvou řad, ale očekává se, že dodáme jen jednu mocninnou řadu. Posledním krokem je tedy spojení oněch dvou řad. Všimněte si ale, že kdybychom je teď sečetli, dostali bychom řadu s rozdílnými mocninami výrazu (x − 1), a tudíž bychom ji nemohli přepsat jako jednu mocninnou řadu. Musíme proto nejprve změnit index v první řadě tak, aby tam byla také mocnina k, což se udělá posunem indexu o 1. Formálně vzato uvedeme jiný index (řekněme n) daný n = k + 1 a pak se zase vrátíme k tradičnímu k prostou záměnou.

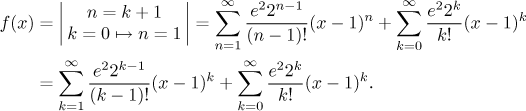
Obě řady teď mají stejnou mocninu u x, ale mají různé indexování. Vidíme, že druhá suma má jeden člen navíc (když je k = 0), takže jej z řady vydělíme a (po drobné kosmetické úpravě) dostaneme "správnou" odpověď.

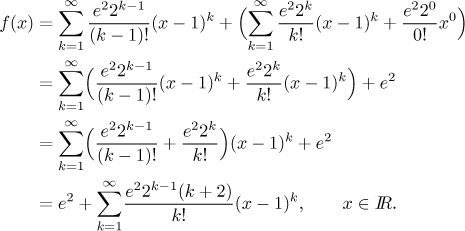
Poznámka: Jaký má smysl vyrábět jednu řadu, když nám to dalo tolik práce? Když pracujeme s řadami, často se potřebuje znát koeficient před třeba (x − 1)¹⁷. To se snadno zjistí z naší konečné odpovědi, ale kdybychom ji nechali jako součet několika řad, pak bychom je museli všechny prohledat ohledně výskytu (x − 1)¹⁷ a pak sečíst odpovídající koeficienty. To je vlastně přesně proces, který jsme před chvílí dělali obecně, dávali jsme dohromady odpovídající mocniny ze všech míst, kde se mohly objevit. Tento postup (který začátečníkům často přijde docela těžký) se zdá mnohem snažší, pokud si umíte představit, co se vlastně děje. Jinými slovy, dobře na to uvidíme, když řadu zapíšeme dlouhým způsobem.

Další příklad
Zpět na Řešené příklady - Řady funkcí